Bir ikili ağacın yüksekliği veya derinliği, bir yaprak düğümden kök düğüme veya kök düğümden yaprak düğüme kadar olan maksimum veya en büyük kenar sayısı olarak tanımlanabilir. Kök düğüm sıfır seviyesinde olacaktır; bu, kök düğümün kendisine bağlı alt düğümlerden herhangi birine sahip olmaması durumunda, söz konusu ikili ağacın yüksekliğinin veya derinliğinin sıfır olduğu söyleneceği anlamına gelir.
İkili ağacın yüksekliğinin daha iyi anlaşılması için bir örnek verelim.
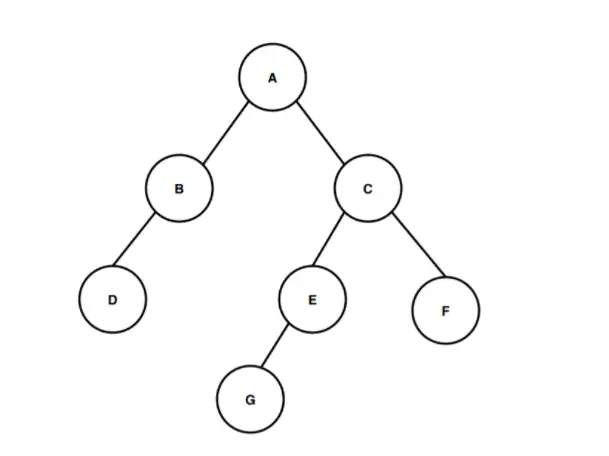
Yukarıdaki görüntüde, A adlı kök düğümden başlayan bir ikili ağacımız var. A kök düğümü, sırasıyla sol çocuk ve sağ çocuk olarak iki alt düğüm B ve C'ye sahiptir. Benzer şekilde, sol alt düğüm B'nin D adında yalnızca bir sol alt düğümü vardır ve sağ alt düğüm C'nin iki alt düğümü E ve F vardır ve E düğümü, tek sol alt çocuk olarak G düğümüne sahiptir.
char'ı string java'ya nasıl dönüştürebilirim?
Şimdi bu ikili ağacın yüksekliğini hesaplayalım. İkili ağacın yüksekliğini hesaplamak için kök düğümden başlayarak en derin yaprak düğüme kadar olan kenar sayısını sayın. Bu ikili ağaçta bulunan en derin düğüm, G düğümüdür. Dolayısıyla, bu ikili ağacın yüksekliğinin veya derinliğinin hesaplanması için, kök düğüm ile en derindeki G düğümü arasındaki kenar sayısını hesaplamamız gerekir. İlk kenar A düğümünden C düğümüne, ikinci kenar C düğümünden E düğümüne ve üçüncü kenar E düğümünden G düğümüne doğrudur. Yani, kök düğüm A'dan en derin G düğümüne geçmek için üç kenar vardır yani ikili ağacın yüksekliği veya derinliği 3'tür. Kökten en derin yaprak düğümüne gitmek için izlediğimiz yol A > C > E > G'dir ve bu yol, geçiş sırasında üç kenarı kapsar, bu nedenle göre İkili ağacın yüksekliğinin tanımına göre bu ikili ağacın yüksekliği 3'tür.
İkili Ağacın Yüksekliğini Bulma Yolları
Şimdi ikili ağacın yüksekliğini bulan kodu yazalım. İkili ağacın yüksekliğini bulmanın iki yolu vardır. Biri yinelemeli yöntem ve diğeri yinelemeli olmayan yöntem bu, ikili ağacın yüksekliğini hesaplamak için Kuyruk veri yapısını kullanacak.
Özyinelemeli Yol
Öncelikle ikili ağacın yüksekliğini bulmanın yinelemeli yolunu görelim.
Kod:
// Java program to create and to find the height of a binary tree by recursive way // util package is imported to use classes like Queue and LinkedList import java.util.*; // A class named Node is created representing a single node of a binary tree class Node{ // The class Node has three class variables named key and left and right of int type and Node type respectively. // the key variable holds the actual value that is assigned to that node of the binary tree int key; // left and right variables that are of Node type will be used to store the left and right child nodes of the parent of the binary tree Node left, right; // a parameterized constructor is created to create and add data to the node at the same time. public Node(int item) { key = item; left = right = null; } } // end of node class definition // A public class named BinaryTree is created having two constructors and methods to print the binary tree level-wise. class BinaryTree{ // A static variable named root_node is created that will represent the node of the binary tree static Node root_node; // A parametrized constructor of the BinaryTree class is written having the key as a parameter BinaryTree(int key) { // here we are constructing a new node and assigning it to the root node root_node = new Node(key); } BinaryTree() { root_node = null; } // a public static function named print tree is created to print all the nodes in the tree level-wise starting from the root node public static void printTree() { int h = height(root_node); int i; for (i=1; i<=h; i++){ printcurrentlevel(root_node, i); system.out.println(); } a public static function named height is created to fund the of binary tree starting from root node deepest leaf that present in passed as parameter called recursively until returned null find int height(node root){ then will be zero if (root="=" null) return 0; else { * compute each subtree lheight="height(root.left);" rheight="height(root.right);" use larger one both sub trees calcualted and which higher used. (lheight> rheight) return(lheight+1); else return(rheight+1); } } // a Public static function named printCurrentLevel is created to print al the nodes that are present in that level // this function is called repeatedly for each level of the binary tree to print all the nodes in that particular level public static void printCurrentLevel (Node root ,int level) { if (root == null) return; if (level == 1) System.out.print(root.key + ' '); else if (level > 1) { printCurrentLevel(root.left, level-1); printCurrentLevel(root.right, level-1); } } //the main function is created to create an object of the BinaryTree class and call the printTree method to level-wise print the nodes of the binary tree and the height method to find the height of the binary tree public static void main(String[] args){ // first of all we have created an Object of the BinaryTree class that will represent the binary tree BinaryTree tree = new BinaryTree(); // now a new node with the value as 150 is added as the root node to the Binary Tree tree.root_node = new Node(150); // now a new node with the value 250 is added as a left child to the root node tree.root_node.left = new Node(250); // now a new node with the value 270 is added as a right child to the root node tree.root_node.right = new Node(270); // now a new node with the value 320 is added as a left child to the left node of the previous level node tree.root_node.left.left = new Node(320); // now a new node with the value 350 is added as a right child to the right node of the previous level node tree.root_node.left.right = new Node(350); /* 150 / 250 270 / / 320 350 null null */ System.out.println('Printing the nodes of tree level wise :'); System.out.println('Level order traversal : '); tree.printTree(); // height of the binary tree is calculated bypassing the root as parameter to the height() function. int h = tree.height(tree.root_node) System.out.println('The height of the Binary tree is : ' + h ); } } // end of the BinaryTree class </=h;> Çıktı: Yukarıdaki kodun çıktısı şöyledir:
Printing the nodes of tree level wise: Level order traversal: (level 0) 150 (level 1) 250 270 (level 2) 320 350 The height of the Binary tree is: 2
Özyinelemeli bir şekilde, biz şunu çağırdık: yükseklik() ikili ağacın yüksekliğini bulmak için tekrar tekrar işlev görür. İkili ağacın kök düğümü, height() işlevine parametre olarak aktarılır. Height() işlevi, kök düğümün her iki alt ağacının yüksekliğini hesaplar ve her iki yükseklikten hangisi daha yüksekse, ikili ağacın yüksekliği olarak kabul edilir.
Yinelemeli Olmayan Yol
Şimdi ikili ağacın yüksekliğini bulmanın yinelemeli olmayan yolunu görelim.
Kod:
java mysql ile bağlantı kurmak
// A C++ program to create and to find the height of a binary tree by non recursive way // iostream header file is included to use the cin and cout objects of the istream and ostream classes respectively #include #include using namespace std; // A struct named Node is created representing a single node of a binary tree struct Node { // The struct Node has three variables named key and left and right of int type and Node type respectively. // the key variable holds the actual value that is assigned to that node of the binary tree int key; // left and right variables that are of Node type will be used to store the left and right child nodes of the parent of the binary tree struct Node* left, *right; }; // A Function named newNode is created to add a new node to the binary tree, the newNode function has one parameter of integer type named key that will represent the value that particular new node will be storing Node* newNode(int key) { Node* temp = new Node; temp->key = key; temp->left = temp->right = NULL; return (temp); } // A function named height is created to find the height of the binary tree with non recursive way // The parameter to the height function is the root node of the binary tree that will be present at level zero // In the height function the nodes of the binary tree are added into the Queue data structure and the depth variable is incremented until // the NULL node is encountered while traversing the nodes of the binary tree stored in the Queue data structure. int height(struct Node* root){ //Initialising a variable to count the //height of tree int depth = 0; queueq; //Pushing first level element along with NULL q.push(root); q.push(NULL); while(!q.empty()){ Node* temp = q.front(); q.pop(); //When NULL encountered, increment the value if(temp == NULL){ depth++; } //If NULL not encountered, keep moving if(temp != NULL){ if(temp->left){ q.push(temp->left); } if(temp->right){ q.push(temp->right); } } //If queue still have elements left, //push NULL again to the queue. else if(!q.empty()){ q.push(NULL); } } return depth; } // Start of the main function int main() { // first of all we have created an Object of the struct Node that will represent the binary tree // the value of the root node is 10 Node *root = newNode(10); // now a new node with the value 20 is added as a left child to the root node root->left = newNode(20); // now a new node with the value 30 is added as a right child to the root node root->right = newNode(30); // now a new node with the value 40 is added as a left child to the left node of the previous level node root->left->left = newNode(40); // now a new node with the value 50 is added as a right child to the left node of the previous level node root->left->right = newNode(50); /* 10 / 20 30 / / 40 50 null null */ cout<<'the height(depth) of tree is: '<<height(root); cout<<endl; } end the main function < pre> <p> <strong>Output:</strong> </p> <pre> The Height(Depth) of the tree is: 2 </pre> <p>In this approach, we have used a non recursive way to find the depth of the binary tree. To find the height of the binary tree, we have written a function named height that will require a parameter of Node type (that means the root of the binary tree whose height needs to be calculated). The root of the binary tree is present at level zero, which means the height or depth of the root is zero.</p> <p>In the non recursive approach, we use the Queue Data Structure to find the depth of the binary tree. The nodes of the binary tree for which we want to find the depth are added to the Queue data structure with the help of an enqueue operation to which the node of the binary tree is passed as a parameter to this function.</p> <p>Once all the nodes are added to the queue, the nodes added in the queue are removed by calling the dequeue function that will keep on removing one element from the queue until the null node of the binary tree is encountered. Each time a node of the binary tree from the queue is removed, the depth variable representing the depth of the binary tree is incremented by one. And in the end, the value of the depth variable will represent the final depth of the binary tree.</p> <hr></'the> Bu yaklaşımda ikili ağacın derinliğini bulmak için yinelemeli olmayan bir yol kullandık. İkili ağacın yüksekliğini bulmak için Node tipinde bir parametreye (yani yüksekliğinin hesaplanması gereken ikili ağacın köküne) ihtiyaç duyacak height adında bir fonksiyon yazdık. İkili ağacın kökü sıfır düzeyinde bulunur, bu da kökün yüksekliğinin veya derinliğinin sıfır olduğu anlamına gelir.
Özyinelemeli olmayan yaklaşımda ikili ağacın derinliğini bulmak için Kuyruk Veri Yapısını kullanırız. Derinliğini bulmak istediğimiz ikili ağacın düğümleri, bu fonksiyona parametre olarak ikili ağacın düğümünün iletildiği sıraya alma işlemi yardımıyla Queue veri yapısına eklenir.
Tüm düğümler kuyruğa eklendikten sonra, ikili ağacın boş düğümüyle karşılaşılıncaya kadar kuyruktan bir öğeyi kaldırmaya devam edecek olan dequeue işlevi çağrılarak kuyruğa eklenen düğümler kaldırılır. İkili ağacın bir düğümü kuyruktan her çıkarıldığında, ikili ağacın derinliğini temsil eden derinlik değişkeni bir artırılır. Ve sonunda derinlik değişkeninin değeri ikili ağacın son derinliğini temsil edecektir.
