Anlamadan önce B ağacı Ve B+ ağacı Farklılıklar için B ağacını ve B+ ağacını ayrı ayrı bilmeliyiz.
B ağacı nedir?
B ağacı kendi kendini dengeleyen bir ağaçtır ve m'nin ağacın sırasını tanımladığı m-yollu bir ağaçtır. Bağacı bir genellemesidir İkili Arama ağacı değerine bağlı olarak bir düğümün birden fazla anahtarı ve ikiden fazla çocuğu olabilir. M . B ağacında veriler, sol alt ağaçta daha düşük değerlere ve sağ alt ağaçta daha yüksek değerlere sahip olacak şekilde sıralanmış bir düzende belirtilir.
rastgele sql'ye göre sırala
B ağacının özellikleri
B ağacının özellikleri şunlardır:
- B ağacında tüm yaprak düğümlerin aynı seviyede olması gerekirken ikili ağaçta yaprak düğümler farklı seviyelerde olabilir.
Bu özelliği bir örnek üzerinden anlayalım.
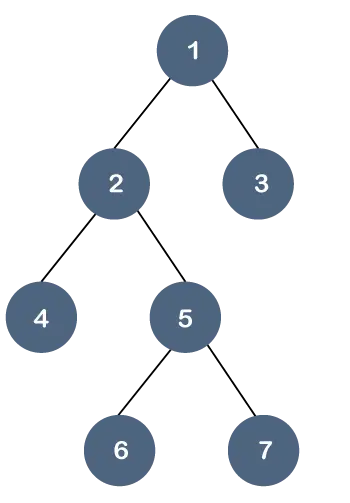
Yukarıdaki ağaçta tüm yaprak düğümleri aynı seviyede değildir ancak en fazla iki çocuğu vardır. Bu nedenle yukarıdaki ağacın bir olduğunu söyleyebiliriz. ikili ağaç ama bir B ağacı değil.
- Btree'nin sırası m ise, her düğümün maksimum değeri olabilir. M Minimum çocuk olması durumunda, yaprak düğümlerin sıfır çocuğu vardır, kök düğümün iki çocuğu vardır ve iç düğümlerin tavanı m/2'dir.
- Her düğümde maksimum (m-1) anahtar bulunabilir. Örneğin m değeri 5 ise tuşların maksimum değeri 4 olur.
- Kök düğümün minimum bir anahtarı vardır, kök düğüm dışındaki diğer tüm düğümlerin ise (m/2 eksi - 1 tavanı) minimum anahtarları vardır.
- B ağacına ekleme yaparsak, düğüm her zaman yaprak düğüme eklenir.
1'den 10'a kadar değerler ekleyerek 3. dereceden bir B ağacı oluşturmak istediğimizi varsayalım.
Aşama 1: Öncelikle aşağıda gösterildiği gibi 1 değerli bir düğüm oluşturuyoruz:

Adım 2: Bir sonraki eleman aşağıda gösterildiği gibi 1'den sonra gelen 2'dir:

Aşama 3: Bir sonraki eleman 3'tür ve aşağıda gösterildiği gibi 2'den sonra eklenir:

Her düğümün maksimum 2 anahtarı olabileceğini bildiğimiz için bu düğümü ortadaki elemana böleceğiz. Ortadaki eleman 2 olduğundan ebeveynine doğru hareket eder. Düğüm 2'nin herhangi bir ebeveyni yoktur, dolayısıyla aşağıda gösterildiği gibi kök düğüm olacaktır:

Adım 4: Bir sonraki eleman 4'tür. 4, 2 ve 3'ten büyük olduğundan aşağıda gösterildiği gibi 3'ten sonra eklenecektir:

Adım 5: Bir sonraki eleman 5'tir. 5, 2, 3 ve 4'ten büyük olduğundan aşağıda gösterildiği gibi 4'ten sonra eklenecektir:

Her düğümün maksimum 2 anahtarı olabileceğini bildiğimiz için bu düğümü ortadaki elemana böleceğiz. Ortadaki eleman 4 olduğundan ebeveynine doğru hareket eder. Ebeveyn düğüm 2'dir; bu nedenle aşağıda gösterildiği gibi 2'den sonra 4 eklenecektir:

Adım 6: Bir sonraki eleman 6'dır. 6, 2, 4 ve 5'ten büyük olduğundan, aşağıda gösterildiği gibi 6, 5'ten sonra gelecektir:

Adım 7: Bir sonraki eleman 7'dir. 7, 2, 4, 5 ve 6'dan büyük olduğundan, aşağıda gösterildiği gibi 6'dan sonra 7 gelecektir:

Her düğümün maksimum 2 anahtarı olabileceğini bildiğimiz için bu düğümü ortadaki elemana böleceğiz. Ortadaki eleman 6'dır, dolayısıyla aşağıda gösterildiği gibi ebeveynine doğru hareket eder:

Ancak 4'ten sonra 6 eklenemez çünkü düğümün maksimum 2 anahtarı olabilir, bu nedenle bu düğümü ortadaki eleman aracılığıyla böleceğiz. Ortadaki eleman 4 olduğundan ebeveynine doğru hareket eder. Düğüm 4'ün herhangi bir ebeveyni olmadığından, düğüm 4 aşağıda gösterildiği gibi bir kök düğüm haline gelecektir:

B+ ağacı nedir?
B+ ağacı Ağacın kökünden yaprağına kadar her yolun aynı uzunlukta olması nedeniyle gelişmiş kendi kendine dengeli ağaç olarak da bilinir. Burada aynı uzunluk, tüm yaprak düğümlerin aynı seviyede meydana geldiği anlamına gelir. Yaprak düğümlerin bir kısmının üçüncü seviyede, bir kısmının ise ikinci seviyede oluşması söz konusu olmayacaktır.
B+ ağaç dizini çok düzeyli bir dizin olarak kabul edilir, ancak B+ ağaç yapısı çok düzeyli dizin sıralı dosyalarına benzemez.
B+ ağacı neden kullanılıyor?
B+ ağacı indeksli yapıyı kullanarak kayıtları indeksli bir şekilde saklayarak kayıtları çok verimli bir şekilde saklamak için bir B+ ağacı kullanılır. Çok seviyeli indeksleme sayesinde verilere erişim daha hızlı ve kolay hale gelir.
B+ ağacı Düğüm Yapısı
B+ ağacının düğüm yapısı aşağıdaki şekilde gösterilen işaretçileri ve anahtar değerleri içerir:

Yukarıdaki B+ ağaç düğüm yapısında gözlemleyebileceğimiz gibi n-1 anahtar değeri (k1k'yen-1) ve n işaretçiler (p1tepeN).
Düğüme yerleştirilen arama anahtarı değerleri sıralı olarak tutulur. Böylece eğer ben
Çeşitli düğüm türlerine ilişkin kısıtlama
'b' B+ ağacının sırası olsun.
Yaprak olmayan düğüm
'm' bir düğümün çocuk sayısını temsil ediyorsa, ağacın sırası ile çocuk sayısı arasındaki ilişki şu şekilde temsil edilebilir:

K'nın arama anahtarı değerlerini temsil etmesine izin verin. Ağacın sırası ile arama anahtarı arasındaki ilişki şu şekilde gösterilebilir:
İşaretçi sayısının arama anahtarı değerleri artı 1'e eşit olduğunu bildiğimiz için matematiksel olarak şu şekilde yazılabilir:
İşaretçi Sayısı (veya alt öğe) = Arama tuşu sayısı + 1
Bu nedenle, maksimum işaretçi sayısı 'b' olacaktır ve minimum işaretçi sayısı b/2'nin tavan fonksiyonu olacaktır.
Yaprak düğümü
Yaprak düğüm, B+ ağacının son seviyesinde oluşan bir düğümdür ve her yaprak düğüm, yaprak düzeyinde sıralı erişim sağlamak amacıyla birbirine bağlanmak için yalnızca bir işaretçi kullanır.
Yaprak düğümde maksimum çocuk sayısı:

Maksimum arama anahtarı sayısı:
disket

Kök Düğüm
Kök düğüm durumunda maksimum çocuk sayısı: b
Minimum çocuk sayısı: 2
B+ ağacındaki özel durumlar
Dava 1: Kök düğüm ağaçtaki tek düğüm ise. Bu durumda kök düğüm yaprak düğüm haline gelir.
Bu durumda maksimum çocuk sayısı 1'dir, yani kök düğümün kendisi, minimum çocuk sayısı ise yaprak düğümünkiyle aynı olan b-1'dir.
B+ ağacındaki yaprak düğümünün temsili

Yukarıdaki şekilde '.' işaretçiyi temsil eder, 10, 20 ve 30 ise anahtar değerlerdir. İşaretçi, yukarıdaki şekilde gösterildiği gibi anahtar değerinin saklandığı adresi içerir.
B+ ağacı örneği

Yukarıdaki şekilde düğüm üç anahtar değer içerir; yani 9, 16 ve 25. 9'dan önce görünen işaretçi, k ile temsil edilen 9'dan küçük anahtar değerleri içerir.Ben. 16'dan önce görünen işaretçi, 9'dan büyük veya ona eşit ancak kj ile temsil edilen 16'dan küçük anahtar değerleri içerir. 25'ten önce görünen işaretçi, 16'dan büyük veya ona eşit ancak k ile temsil edilen 25'ten küçük anahtar değerleri içerir.N.
B ağacı ile B+ ağacı arasındaki farklar

B ağacı ile B+ ağacı arasındaki farklar şunlardır:
| B ağacı | B+ ağacı |
|---|---|
| B ağacında tüm anahtarlar ve kayıtlar hem dahili hem de yaprak düğümlerde depolanır. | B+ ağacında anahtarlar iç düğümlerde saklanan dizinlerdir ve kayıtlar da yaprak düğümlerde depolanır. |
| B ağacında anahtarlar tekrar tekrar saklanamaz; bu, anahtarların veya kayıtların çoğaltılamayacağı anlamına gelir. | B+ ağacında anahtarların oluşumunda fazlalık olabilir. Bu durumda kayıtlar yaprak düğümlerde, anahtarlar ise iç düğümlerde depolanır, böylece yedek anahtarlar iç düğümlerde bulunabilir. |
| Btree'de yaprak düğümler birbirine bağlı değildir. | B+ ağacında yaprak düğümler sıralı erişimi sağlayacak şekilde birbirine bağlanır. |
| Btree'de kayıtlar ya yaprak düğümlerde ya da dahili düğümlerde saklandığından arama çok verimli değildir. | B+ ağacında tüm kayıtlar yaprak düğümlerde saklandığı için arama çok verimli ve hızlıdır. |
| Silinen anahtarın alt öğesini de dikkate almamız gerektiğinden, dahili düğümlerin silinmesi çok yavaş ve zaman alıcı bir süreçtir. | B+ ağacında silme işlemi çok hızlıdır çünkü tüm kayıtlar yaprak düğümlerde depolanır, dolayısıyla düğümün çocuğunu dikkate almamıza gerek kalmaz. |
| Btree'de sıralı erişim mümkün değildir. | B+ ağacında tüm yaprak düğümler bir işaretçi aracılığıyla birbirine bağlanır, böylece sıralı erişim mümkündür. |
| Btree'de yüksekliğin genişliğe göre artması nedeniyle daha fazla bölme işlemi gerçekleştirilir, | B+ ağacının yüksekliğine göre genişliği daha fazladır. |
| Btree'de her düğümün en az iki dalı vardır ve her düğüm bazı kayıtlar içerir, dolayısıyla veriyi almak için yaprak düğümlere kadar gitmemize gerek yoktur. | B+ ağacında iç düğümler yalnızca işaretçileri içerir ve yaprak düğümler kayıtları içerir. Tüm yaprak düğümler aynı seviyede olduğundan veriyi almak için yaprak düğümlere kadar gitmemiz gerekiyor. |
| Kök düğüm en az 2 ile m arasında çocuk içerir; burada m, ağacın sırasıdır. | Kök düğüm en az 2 ile m arasında çocuk içerir; burada m, ağacın sırasıdır. |
