Bu yazımızda İkili arama ağacını tartışacağız. Bu makale, derslerinin önemli bir konusu olduğundan teknik altyapıya sahip öğrenciler için çok yararlı ve bilgilendirici olacaktır.
Doğrudan ikili arama ağacına geçmeden önce ağacın kısa bir açıklamasına bakalım.
Ağaç nedir?
Ağaç, verileri hiyerarşik biçimde temsil etmek için kullanılan bir tür veri yapısıdır. Bir hiyerarşiyi simüle etmek için birbirine bağlanan, düğüm adı verilen nesneler veya varlıklar topluluğu olarak tanımlanabilir. Ağaç, bir ağaçtaki veriler doğrusal veya sıralı olarak depolanmadığından doğrusal olmayan bir veri yapısıdır.
Şimdi konuya, İkili Arama ağacına başlayalım.
İkili Arama ağacı nedir?
Bir ikili arama ağacı, elemanları düzenlemek için belirli bir sırayı takip eder. İkili arama ağacında, sol düğümün değeri üst düğümden küçük olmalı ve sağ düğümün değeri üst düğümden büyük olmalıdır. Bu kural kökün sol ve sağ alt ağaçlarına yinelemeli olarak uygulanır.
Bir örnekle İkili arama ağacı kavramını anlayalım.
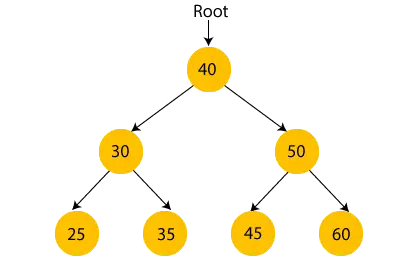
Yukarıdaki şekilde kök düğümün 40 olduğunu, sol alt ağacın tüm düğümlerinin kök düğümden küçük olduğunu ve sağ alt ağacın tüm düğümlerinin kök düğümden büyük olduğunu görebiliriz.
Benzer şekilde, kök düğümün sol çocuğunun, sol çocuğundan daha büyük ve sağ çocuğundan daha küçük olduğunu görebiliriz. Dolayısıyla ikili arama ağacının özelliğini de karşılamaktadır. Dolayısıyla yukarıdaki görseldeki ağacın bir ikili arama ağacı olduğunu söyleyebiliriz.
Yukarıdaki ağaçta 35. düğümün değerini 55 olarak değiştirirsek, ağacın ikili arama ağacı olup olmayacağını kontrol edelim.
java ile bir dosya nasıl açılır

Yukarıdaki ağaçta kök düğümün değeri 40'tır, bu da sol çocuğu 30'dan büyük ancak sağ çocuğu 30'dan küçüktür, yani 55. Dolayısıyla yukarıdaki ağaç İkili arama ağacının özelliğini karşılamaz. Bu nedenle yukarıdaki ağaç bir ikili arama ağacı değildir.
İkili arama ağacının avantajları
- İkili arama ağacında bir öğeyi aramak kolaydır çünkü her zaman hangi alt ağacın istenen öğeye sahip olduğuna dair bir ipucumuz olur.
- Dizi ve bağlantılı listelerle karşılaştırıldığında BST'de ekleme ve silme işlemleri daha hızlıdır.
İkili arama ağacı oluşturma örneği
Şimdi bir örnek kullanarak ikili arama ağacının oluşturulmasını görelim.
Veri öğelerinin olduğunu varsayalım - 45, 15, 79, 90, 10, 55, 12, 20, 50
- İlk önce eklememiz gerekiyor Dört beş ağacın kökü olarak ağaca.
- Ardından bir sonraki öğeyi okuyun; kök düğümden küçükse, onu sol alt ağacın kökü olarak ekleyin ve bir sonraki öğeye geçin.
- Aksi takdirde, eğer öğe kök düğümden büyükse, onu sağ alt ağacın kökü olarak ekleyin.
Şimdi verilen veri öğesini kullanarak İkili arama ağacını oluşturma sürecini görelim. BST oluşturma süreci aşağıda gösterilmiştir:
Adım 1 - 45'i ekleyin.

Adım 2 - 15'i ekleyin.
15, 45'ten küçük olduğundan, onu sol alt ağacın kök düğümü olarak ekleyin.
Java'da arraylist'i sırala

Adım 3 - 79'u ekleyin.
79, 45'ten büyük olduğundan, onu sağ alt ağacın kök düğümü olarak ekleyin.

Adım 4 - 90'ı ekleyin.
90, 45 ve 79'dan büyük olduğundan 79'un sağ alt ağacı olarak eklenecektir.

Adım 5 - 10'u ekleyin.
10, 45 ve 15'ten küçüktür, dolayısıyla 15'in sol alt ağacı olarak yerleştirilecektir.

Adım 6 - 55'i ekleyin.
55, 45'ten büyük ve 79'dan küçüktür, dolayısıyla 79'un sol alt ağacı olarak yerleştirilecektir.

Adım 7 - 12'yi ekleyin.
12, 45 ve 15'ten küçük fakat 10'dan büyüktür, dolayısıyla 10'un sağ alt ağacı olarak eklenir.

Adım 8 - 20'yi ekleyin.
ana yöntem java
20, 45'ten küçük ama 15'ten büyüktür, dolayısıyla 15'in sağ alt ağacı olarak eklenir.

Adım 9 - 50'yi ekleyin.
50, 45'ten büyüktür ancak 79 ve 55'ten küçüktür. Yani 55'in sol alt ağacı olarak yerleştirilecektir.

Artık ikili arama ağacının oluşturulması tamamlandı. Bundan sonra Binary arama ağacı üzerinde yapılabilecek işlemlere geçelim.
İkili arama ağacı üzerinde ekleme, silme ve arama işlemlerini gerçekleştirebiliriz.
İkili arama ağacında aramanın nasıl yapıldığını anlayalım.
İkili arama ağacında arama
Arama, bir veri yapısındaki belirli bir öğeyi veya düğümü bulmak veya bulmak anlamına gelir. İkili arama ağacında bir düğümü aramak kolaydır çünkü BST'deki öğeler belirli bir sırada depolanır. İkili Arama ağacında bir düğümü arama adımları aşağıdaki gibi listelenmiştir:
- Öncelikle aranacak öğeyi ağacın kök öğesiyle karşılaştırın.
- Kök hedef öğeyle eşleşiyorsa düğümün konumunu döndürün.
- Eşleşmiyorsa öğenin kök öğeden küçük olup olmadığını kontrol edin, kök öğeden küçükse sol alt ağaca geçin.
- Kök elemandan büyükse sağ alt ağaca gidin.
- Eşleşme bulunana kadar yukarıdaki prosedürü tekrar tekrar tekrarlayın.
- Öğe ağaçta bulunamazsa veya mevcut değilse NULL değerini döndürün.
Şimdi ikili ağaçta aramayı bir örnekle anlayalım. Yukarıda oluşturulan ikili arama ağacını alıyoruz. Aşağıdaki ağaçtan 20. düğümü bulmamız gerektiğini varsayalım.
Aşama 1:

Adım 2:

Aşama 3:

Şimdi İkili arama ağacında bir öğeyi aramak için kullanılan algoritmayı görelim.
İkili arama ağacında bir öğeyi aramak için algoritma
Search (root, item) Step 1 - if (item = root → data) or (root = NULL) return root else if (item <root 2 → data) return search(root left, item) else right, end if step - < pre> <p>Now let's understand how the deletion is performed on a binary search tree. We will also see an example to delete an element from the given tree.</p> <h3>Deletion in Binary Search tree</h3> <p>In a binary search tree, we must delete a node from the tree by keeping in mind that the property of BST is not violated. To delete a node from BST, there are three possible situations occur -</p> <ul> <li>The node to be deleted is the leaf node, or,</li> <li>The node to be deleted has only one child, and,</li> <li>The node to be deleted has two children</li> </ul> <p>We will understand the situations listed above in detail.</p> <p> <strong>When the node to be deleted is the leaf node</strong> </p> <p>It is the simplest case to delete a node in BST. Here, we have to replace the leaf node with NULL and simply free the allocated space.</p> <p>We can see the process to delete a leaf node from BST in the below image. In below image, suppose we have to delete node 90, as the node to be deleted is a leaf node, so it will be replaced with NULL, and the allocated space will free.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-15.webp" alt="Binary Search tree"> <p> <strong>When the node to be deleted has only one child</strong> </p> <p>In this case, we have to replace the target node with its child, and then delete the child node. It means that after replacing the target node with its child node, the child node will now contain the value to be deleted. So, we simply have to replace the child node with NULL and free up the allocated space.</p> <p>We can see the process of deleting a node with one child from BST in the below image. In the below image, suppose we have to delete the node 79, as the node to be deleted has only one child, so it will be replaced with its child 55.</p> <p>So, the replaced node 79 will now be a leaf node that can be easily deleted.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-16.webp" alt="Binary Search tree"> <p> <strong>When the node to be deleted has two children</strong> </p> <p>This case of deleting a node in BST is a bit complex among other two cases. In such a case, the steps to be followed are listed as follows -</p> <ul> <li>First, find the inorder successor of the node to be deleted.</li> <li>After that, replace that node with the inorder successor until the target node is placed at the leaf of tree.</li> <li>And at last, replace the node with NULL and free up the allocated space.</li> </ul> <p>The inorder successor is required when the right child of the node is not empty. We can obtain the inorder successor by finding the minimum element in the right child of the node.</p> <p>We can see the process of deleting a node with two children from BST in the below image. In the below image, suppose we have to delete node 45 that is the root node, as the node to be deleted has two children, so it will be replaced with its inorder successor. Now, node 45 will be at the leaf of the tree so that it can be deleted easily.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-17.webp" alt="Binary Search tree"> <p>Now let's understand how insertion is performed on a binary search tree.</p> <h3>Insertion in Binary Search tree</h3> <p>A new key in BST is always inserted at the leaf. To insert an element in BST, we have to start searching from the root node; if the node to be inserted is less than the root node, then search for an empty location in the left subtree. Else, search for the empty location in the right subtree and insert the data. Insert in BST is similar to searching, as we always have to maintain the rule that the left subtree is smaller than the root, and right subtree is larger than the root.</p> <p>Now, let's see the process of inserting a node into BST using an example.</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-18.webp" alt="Binary Search tree"> <br> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-19.webp" alt="Binary Search tree"> <h3>The complexity of the Binary Search tree</h3> <p>Let's see the time and space complexity of the Binary search tree. We will see the time complexity for insertion, deletion, and searching operations in best case, average case, and worst case.</p> <h3>1. Time Complexity</h3> <table class="table"> <tr> <th>Operations</th> <th>Best case time complexity</th> <th>Average case time complexity</th> <th>Worst case time complexity</th> </tr> <tr> <td> <strong>Insertion</strong> </td> <td>O(log n)</td> <td>O(log n)</td> <td>O(n)</td> </tr> <tr> <td> <strong>Deletion</strong> </td> <td>O(log n)</td> <td>O(log n)</td> <td>O(n)</td> </tr> <tr> <td> <strong>Search</strong> </td> <td>O(log n)</td> <td>O(log n)</td> <td>O(n)</td> </tr> </table> <p>Where 'n' is the number of nodes in the given tree.</p> <h3>2. Space Complexity</h3> <table class="table"> <tr> <th>Operations</th> <th>Space complexity</th> </tr> <tr> <td> <strong>Insertion</strong> </td> <td>O(n)</td> </tr> <tr> <td> <strong>Deletion</strong> </td> <td>O(n)</td> </tr> <tr> <td> <strong>Search</strong> </td> <td>O(n)</td> </tr> </table> <ul> <li>The space complexity of all operations of Binary search tree is O(n).</li> </ul> <h2>Implementation of Binary search tree</h2> <p>Now, let's see the program to implement the operations of Binary Search tree.</p> <p> <strong>Program:</strong> Write a program to perform operations of Binary Search tree in C++.</p> <p>In this program, we will see the implementation of the operations of binary search tree. Here, we will see the creation, inorder traversal, insertion, and deletion operations of tree.</p> <p>Here, we will see the inorder traversal of the tree to check whether the nodes of the tree are in their proper location or not. We know that the inorder traversal always gives us the data in ascending order. So, after performing the insertion and deletion operations, we perform the inorder traversal, and after traversing, if we get data in ascending order, then it is clear that the nodes are in their proper location.</p> <pre> #include using namespace std; struct Node { int data; Node *left; Node *right; }; Node* create(int item) { Node* node = new Node; node->data = item; node->left = node->right = NULL; return node; } /*Inorder traversal of the tree formed*/ void inorder(Node *root) { if (root == NULL) return; inorder(root->left); //traverse left subtree cout<data <right); traverse right subtree } node* findminimum(node* cur) *to find the inorder successor* { while(cur->left != NULL) { cur = cur->left; } return cur; } Node* insertion(Node* root, int item) /*Insert a node*/ { if (root == NULL) return create(item); /*return new node if tree is empty*/ if (item data) root->left = insertion(root->left, item); else root->right = insertion(root->right, item); return root; } void search(Node* &cur, int item, Node* &parent) { while (cur != NULL && cur->data != item) { parent = cur; if (item data) cur = cur->left; else cur = cur->right; } } void deletion(Node*& root, int item) /*function to delete a node*/ { Node* parent = NULL; Node* cur = root; search(cur, item, parent); /*find the node to be deleted*/ if (cur == NULL) return; if (cur->left == NULL && cur->right == NULL) /*When node has no children*/ { if (cur != root) { if (parent->left == cur) parent->left = NULL; else parent->right = NULL; } else root = NULL; free(cur); } else if (cur->left && cur->right) { Node* succ = findMinimum(cur->right); int val = succ->data; deletion(root, succ->data); cur->data = val; } else { Node* child = (cur->left)? cur->left: cur->right; if (cur != root) { if (cur == parent->left) parent->left = child; else parent->right = child; } else root = child; free(cur); } } int main() { Node* root = NULL; root = insertion(root, 45); root = insertion(root, 30); root = insertion(root, 50); root = insertion(root, 25); root = insertion(root, 35); root = insertion(root, 45); root = insertion(root, 60); root = insertion(root, 4); printf('The inorder traversal of the given binary tree is -
'); inorder(root); deletion(root, 25); printf('
After deleting node 25, the inorder traversal of the given binary tree is -
'); inorder(root); insertion(root, 2); printf('
After inserting node 2, the inorder traversal of the given binary tree is -
'); inorder(root); return 0; } </data></pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/58/binary-search-tree-20.webp" alt="Binary Search tree"> <p>So, that's all about the article. Hope the article will be helpful and informative to you.</p> <hr></root> Çıktı
linux ücretsiz ipconfig
Yukarıdaki kodun yürütülmesinden sonra çıktı şu şekilde olacaktır:

Yani bu makaleyle ilgili. Umarım makale sizin için yararlı ve bilgilendirici olacaktır.
