Bilgisayarların icadından bu yana insanlar 'terimini kullanıyorlar' Veri ' İletilen veya saklanan Bilgisayar Bilgisine atıfta bulunmak için. Ancak emir türlerinde de var olan veriler var. Veriler, elektronik cihazların hafızasında saklanan bit ve bayt şeklinde bir kağıt parçası üzerine yazılan sayılar veya metinler ya da bir kişinin zihninde saklanan gerçekler olabilir. Dünya modernleşmeye başladıkça bu veriler herkesin günlük yaşamının önemli bir parçası haline geldi ve çeşitli uygulamalar, bu verilerin farklı şekilde saklanmasına olanak sağladı.

Veri tek bir öğe değerleri kümesine atıfta bulunan, gerçekler ve rakamlardan oluşan bir koleksiyon veya belirli bir formattaki değerler veya değerler kümesidir. Veri öğeleri daha sonra, öğenin basit birincil biçimi olarak bilinmeyen öğe grubu olan alt öğeler halinde sınıflandırılır.

Bir çalışan adının üç alt öğeye bölünebildiği bir örneği ele alalım: İlk, Orta ve Son. Ancak bir çalışana atanan kimlik genellikle tek bir öğe olarak değerlendirilecektir.

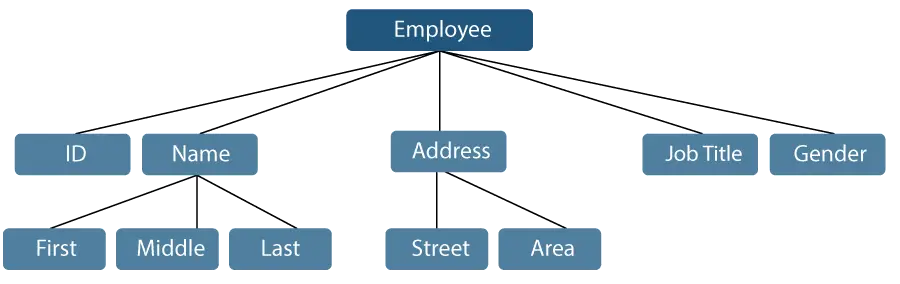
Şekil 1: Veri Öğelerinin Temsili

Yukarıda bahsedilen örnekte Kimlik, Yaş, Cinsiyet, Ad, Orta, Soyadı, Sokak, Mahalle vb. öğeler temel veri öğeleridir. Bunun aksine, Ad ve Adres grup veri öğeleridir.

Veri Yapısı Nedir?

Veri yapısı Bilgisayar Bilimlerinin bir dalıdır. Veri yapısının incelenmesi, herhangi bir süreç veya programın verimliliğini artırmak için verilerin organizasyonunu ve veri akışının yönetimini anlamamızı sağlar. Veri Yapısı, verileri bilgisayarın belleğinde saklamanın ve düzenlemenin özel bir yoludur; böylece bu veriler gelecekte gerektiğinde kolayca alınabilir ve verimli bir şekilde kullanılabilir. Veriler, veri yapısı olarak bilinen belirli bir veri organizasyonu için mantıksal veya matematiksel model gibi çeşitli şekillerde yönetilebilir.

Belirli bir veri modelinin kapsamı iki faktöre bağlıdır:

1. İlk olarak, verinin gerçek dünyadaki bir nesneyle kesin korelasyonunu yansıtacak kadar yapıya yeterince yüklenmiş olması gerekir.
2. İkincisi, formasyon o kadar basit olmalı ki gerektiğinde veriyi verimli bir şekilde işlemeye uyum sağlanabilsin.

Veri Yapılarının bazı örnekleri Diziler, Bağlantılı Listeler, Yığın, Kuyruk, Ağaçlar vb.'dir. Veri Yapıları, Bilgisayar Biliminin hemen hemen her alanında, yani Derleyici Tasarımı, İşletim Sistemleri, Grafikler, Yapay Zeka ve daha pek çok alanda yaygın olarak kullanılmaktadır.

Veri Yapıları, programcıların verileri etkili bir şekilde yönetmelerine olanak tanıdığından, birçok Bilgisayar Bilimi Algoritmasının ana parçasıdır. Yazılımın temel amacı kullanıcının verilerini mümkün olduğu kadar hızlı depolamak ve almak olduğundan, bir programın veya yazılımın performansını artırmada çok önemli bir rol oynar.

c'de statik

Veri Yapılarıyla İlgili Temel Terminolojiler

Veri Yapıları herhangi bir yazılım veya programın yapı taşlarıdır. Bir program için uygun veri yapısını seçmek programcı için son derece zorlu bir iştir.

Veri yapıları söz konusu olduğunda kullanılan bazı temel terminolojiler aşağıda verilmiştir:

Veri:Veriyi temel bir değer veya bir değerler topluluğu olarak tanımlayabiliriz. Örneğin Çalışanın adı ve kimliği Çalışana ilişkin verilerdir.Veri Öğeleri:Tek bir değer birimi Veri Öğesi olarak bilinir.Grup Öğeleri:Alt veri öğelerine sahip Veri Öğeleri, Grup Öğeleri olarak bilinir. Örneğin, bir çalışanın adı bir ad, ikinci ad ve soyadına sahip olabilir.Temel Öğeler:Alt öğelere bölünemeyen Veri Öğeleri, Temel Öğeler olarak bilinir. Örneğin, bir Çalışanın kimliği.Varlık ve Nitelik:Belirli nesnelerin bir sınıfı bir Varlık tarafından temsil edilir. Farklı Niteliklerden oluşur. Her Nitelik, o Varlığın spesifik özelliğini sembolize eder. Örneğin,

Benzer özelliklere sahip varlıklar bir Varlık Seti . Bir varlık kümesinin her niteliği, belirli bir niteliğe atanabilecek tüm olası değerlerin kümesi olan bir değer aralığına sahiptir.

'Bilgi' terimi bazen anlamlı veya işlenmiş verinin belirli niteliklerine sahip veriler için kullanılır.

Alan:Bir Varlığın Niteliğini simgeleyen tek bir temel bilgi birimi Alan olarak bilinir.Kayıt:Farklı veri öğelerinden oluşan bir koleksiyon Kayıt olarak bilinir. Örneğin, çalışan varlığı hakkında konuşursak, çalışanın kaydını oluşturmak için adı, kimliği, adresi ve iş unvanı gruplandırılabilir.Dosya:Bir varlık tipindeki farklı Kayıtların koleksiyonu Dosya olarak bilinir. Örneğin 100 çalışan varsa ilgili dosyada her çalışana ait bilgilerin yer aldığı 25 kayıt bulunacaktır.

Veri Yapılarına Olan İhtiyacı Anlamak

Uygulamalar daha karmaşık hale geldikçe ve veri miktarı her geçen gün arttıkça, bu durum veri arama, işlem hızı, çoklu isteklerin işlenmesi ve daha pek çok konuda sorunlara yol açabilir. Veri Yapıları, verileri verimli bir şekilde düzenlemek, yönetmek ve depolamak için farklı yöntemleri destekler. Veri Yapılarının yardımıyla veri öğelerini kolayca dolaşabiliriz. Veri Yapıları Verimlilik, Yeniden Kullanılabilirlik ve Soyutlama sağlar.

Neden Veri Yapılarını öğrenmeliyiz?

1. Veri Yapıları ve Algoritmalar Bilgisayar Biliminin temel yönlerinden ikisidir.
2. Veri Yapıları verileri düzenlememize ve saklamamıza olanak tanırken, Algoritmalar bu verileri anlamlı bir şekilde işlememize olanak tanır.
3. Veri Yapılarını ve Algoritmalarını öğrenmek, daha iyi Programcılar olmamıza yardımcı olacaktır.
4. Daha etkili ve güvenilir kod yazabileceğiz.
5. Ayrıca sorunları daha hızlı ve verimli bir şekilde çözebileceğiz.

Veri Yapılarının Amaçlarını Anlamak

Veri Yapıları iki tamamlayıcı hedefi karşılar:

Doğruluk:Veri Yapıları, ilgi alanına bağlı olarak her türlü girdi için doğru şekilde çalışacak şekilde tasarlanmıştır. Başka bir deyişle doğruluk, her zaman Veri Yapısının çözmesi gereken sorunlara bağlı olan Veri Yapısının temel amacını oluşturur.Yeterlik:Veri Yapıları aynı zamanda verimli olmayı da gerektirir. Bellek alanı gibi birçok bilgisayar kaynağını kullanmadan verileri hızlı bir şekilde işlemelidir. Gerçek zamanlı durumda, bir veri yapısının verimliliği, sürecin başarısını ve başarısızlığını belirlemede önemli bir faktördür.

Veri Yapılarının Bazı Temel Özelliklerini Anlamak

Veri Yapılarının Önemli Özelliklerinden Bazıları şunlardır:

git'te ödeme

Sağlamlık:Genel olarak tüm bilgisayar programcıları, tüm donanım platformlarında etkin yürütmenin yanı sıra, olası her giriş için doğru çıktı sağlayan yazılımlar üretmeyi amaçlar. Bu tür sağlam bir yazılımın hem geçerli hem de geçersiz girişleri yönetmesi gerekir.Uyarlanabilirlik:Web Tarayıcıları, Kelime İşlemciler ve İnternet Arama Motoru gibi yazılım uygulamaları oluşturmak, uzun yıllar boyunca doğru ve verimli çalışmayı veya yürütülmesini gerektiren devasa yazılım sistemlerini içerir. Üstelik yazılımlar gelişen teknolojilere veya sürekli değişen pazar koşullarına bağlı olarak gelişiyor.Tekrar Kullanılabilirlik:Yeniden Kullanılabilirlik ve Uyarlanabilirlik gibi özellikler el ele gider. Programcının herhangi bir yazılımı oluşturmak için birçok kaynağa ihtiyaç duyduğu ve bunun da onu maliyetli bir girişim haline getirdiği bilinmektedir. Ancak yazılım yeniden kullanılabilir ve uyarlanabilir bir şekilde geliştirilirse gelecekteki uygulamaların çoğuna uygulanabilir. Böylece kaliteli veri yapılarını uygulayarak, maliyet etkin ve zaman tasarrufu sağlayan yeniden kullanılabilir yazılımlar oluşturmak mümkündür.

Veri Yapılarının Sınıflandırılması

Veri Yapısı, çeşitli yollarla birbiriyle ilişkili yapılandırılmış bir değişkenler kümesi sunar. Veri öğeleri arasındaki ilişkiyi belirten ve programcıların verileri verimli bir şekilde işlemesine olanak tanıyan bir programlama aracının temelini oluşturur.

Veri Yapılarını iki kategoriye ayırabiliriz:

1. İlkel Veri Yapısı
2. İlkel Olmayan Veri Yapısı

Aşağıdaki şekil Veri Yapılarının farklı sınıflandırmalarını göstermektedir.

Şekil 2: Veri Yapılarının Sınıflandırmaları

İlkel Veri Yapıları

İlkel Veri Yapılarıgelen sayı ve karakterlerden oluşan veri yapılarıdır dahili programlara dönüştürülür.
1. Bu veri yapıları doğrudan makine düzeyindeki talimatlarla değiştirilebilir veya çalıştırılabilir.
2. Gibi temel veri türleri Tam Sayı, Kayan Nokta, Karakter , Ve Boolean İlkel Veri Yapıları kapsamına girer.
3. Bu veri türlerine aynı zamanda denir. Basit veri türleri daha fazla bölünemeyen karakterler içerdiklerinden

İlkel Olmayan Veri Yapıları

İlkel Olmayan Veri Yapılarıİlkel Veri Yapılarından türetilen veri yapılarıdır.
1. Bu veri yapıları doğrudan makine düzeyindeki talimatlarla değiştirilemez veya çalıştırılamaz.
2. Bu veri yapılarının odak noktası, bir dizi veri elemanı oluşturmaktır. homojen (aynı veri türü) veya heterojen (farklı veri türleri).
3. Verilerin yapısına ve düzenine bağlı olarak bu veri yapılarını iki alt kategoriye ayırabiliriz:
   1. Doğrusal Veri Yapıları
   2. Doğrusal Olmayan Veri Yapıları

Doğrusal Veri Yapıları

Veri öğeleri arasındaki doğrusal bağlantıyı koruyan bir veri yapısı, Doğrusal Veri Yapısı olarak bilinir. Verilerin düzenlenmesi doğrusal olarak yapılır; burada her öğe, ilk ve son veri öğesi dışındaki ardıllardan ve öncüllerden oluşur. Bununla birlikte, düzenleme sıralı olmayabileceğinden, bellek durumunda bu mutlaka doğru değildir.

Bellek tahsisine bağlı olarak Doğrusal Veri Yapıları ayrıca iki türe ayrılır:

Statik Veri Yapıları:Sabit bir boyuta sahip olan veri yapıları Statik Veri Yapıları olarak bilinir. Bu veri yapılarının belleği derleyici zamanında tahsis edilir ve boyutları derlendikten sonra kullanıcı tarafından değiştirilemez; ancak içlerinde saklanan veriler değiştirilebilir.
Sıralamak Sabit bir boyuta sahip olmaları ve verilerinin daha sonra değiştirilebilmesi nedeniyle Statik Veri Yapısının en iyi örneğidir.Dinamik Veri Yapıları:Dinamik boyuta sahip veri yapıları Dinamik Veri Yapıları olarak bilinir. Bu veri yapılarının hafızası çalışma zamanında tahsis edilir ve boyutları kodun çalışma süresi boyunca değişir. Ayrıca kullanıcı, kodun çalışma anında bu veri yapılarında saklanan veri elemanlarının yanı sıra boyutunu da değiştirebilmektedir.
Bağlantılı Listeler, Yığınlar , Ve Kuyruklar dinamik veri yapılarının yaygın örnekleridir

Doğrusal Veri Yapılarının Türleri

Genel olarak kullandığımız Doğrusal Veri Yapılarının listesi aşağıdadır:

1. Diziler

Bir Sıralamak Aynı veri tipindeki birden fazla veri öğesini tek bir değişkende toplamak için kullanılan bir veri yapısıdır. Aynı veri tipinin birden fazla değerini ayrı değişken adlarında saklamak yerine, hepsini tek bir değişkende saklayabiliriz. Bu ifade, herhangi bir programdaki aynı veri tipindeki tüm değerleri, o veri tipindeki tek bir dizide birleştirmemiz gerektiği anlamına gelmez. Ancak aynı veri tipindeki bazı spesifik değişkenlerin hepsinin bir diziye uygun bir şekilde birbiriyle ilişkili olduğu zamanlar da sıklıkla olacaktır.

Dizi, her öğenin listede benzersiz bir yere sahip olduğu öğelerin listesidir. Dizinin veri öğeleri aynı değişken adını paylaşır; ancak her biri alt simge adı verilen farklı bir dizin numarası taşır. Listedeki herhangi bir veri öğesine listedeki konumu yardımıyla erişebiliriz. Bu nedenle, dizilerin anlaşılması gereken temel özelliği, verilerin bitişik bellek konumlarında saklanması ve kullanıcıların ilgili dizinleri kullanarak dizinin veri öğeleri arasında geçiş yapmasına olanak sağlamasıdır.

Figür 3. Bir Dizi

Diziler farklı tiplere ayrılabilir:

Tek Boyutlu Dizi:Yalnızca bir satır veri öğesi içeren bir Dizi, Tek Boyutlu Dizi olarak bilinir. Artan depolama konumunda saklanır.İki Boyutlu Dizi:Veri öğelerinin birden fazla satırından ve sütunundan oluşan bir Diziye İki Boyutlu Dizi adı verilir. Aynı zamanda Matrix olarak da bilinir.Çok Boyutlu Dizi:Çok Boyutlu Diziyi Diziler Dizisi olarak tanımlayabiliriz. Çok Boyutlu Diziler, ihtiyaca göre çok sayıda indeks içerebildiği için iki indekse veya iki boyuta bağlı değildir.

Dizinin Bazı Uygulamaları:

Gimp arka planı siliyor

1. Aynı veri tipine ait veri elemanlarının bir listesini saklayabiliriz.
2. Dizi, diğer veri yapıları için yardımcı depolama görevi görür.
3. Dizi aynı zamanda sabit sayıdaki ikili ağacın veri öğelerinin depolanmasına da yardımcı olur.
4. Dizi aynı zamanda matrislerin depolanması görevi de görür.

2. Bağlantılı Listeler

A Bağlantılı liste bir veri öğeleri koleksiyonunu dinamik olarak depolamak için kullanılan doğrusal veri yapısının başka bir örneğidir. Bu veri yapısındaki veri öğeleri, bağlantılar veya işaretçiler kullanılarak bağlanan Düğümler tarafından temsil edilir. Her düğüm iki alan içerir; bilgi alanı gerçek verilerden oluşur ve işaretçi alanı listedeki sonraki düğümlerin adresinden oluşur. Bağlantılı listenin son düğümünün işaretçisi, hiçbir şeye işaret etmediği için boş bir işaretçiden oluşur. Dizilerden farklı olarak kullanıcı, Bağlantılı Listenin boyutunu gereksinimlere göre dinamik olarak ayarlayabilir.

Şekil 4. Bağlantılı Liste

Bağlantılı Listeler farklı türlere ayrılabilir:

Tek Bağlantılı Liste:Tek Bağlantılı Liste, Bağlantılı Listelerin en yaygın türüdür. Her düğümün verileri ve bir sonraki düğümün adresini içeren bir işaretçi alanı vardır.Çift Bağlantılı Liste:Çift Bağlantılı Liste, bir bilgi alanı ve iki işaretçi alanından oluşur. Bilgi alanı verileri içerir. İlk işaretçi alanı önceki düğümün adresini içerirken, başka bir işaretçi alanı bir sonraki düğüme referans içerir. Böylece her iki yöne de gidebiliriz (ileriye olduğu kadar geriye de).Dairesel Bağlantılı Liste:Dairesel Bağlantılı Liste, Tek Bağlantılı Listeye benzer. Tek önemli fark, son düğümün ilk düğümün adresini içermesi ve Dairesel Bağlantılı Listede dairesel bir döngü oluşturmasıdır.

Bağlantılı Listelerin Bazı Uygulamaları:

1. Bağlantılı Listeler yığınları, kuyrukları, ikili ağaçları ve önceden tanımlanmış boyuttaki grafikleri uygulamamıza yardımcı olur.
2. Dinamik bellek yönetimi için İşletim Sisteminin işlevini de uygulayabiliriz.
3. Bağlantılı Listeler ayrıca matematiksel işlemler için polinom uygulamasına da izin verir.
4. Görevlerin Round Robin tarafından yürütülmesini sağlayan İşletim Sistemlerini veya uygulama işlevlerini uygulamak için Dairesel Bağlantılı Listeyi kullanabiliriz.
5. Dairesel Bağlantılı Liste, kullanıcının son slayt sunulduktan sonra ilk slayda geri dönmesini gerektiren Slayt Gösterisinde de faydalıdır.
6. Çift Bağlantılı Liste, bir web sitesinin açılan sayfalarında ileri ve geri gitmek için tarayıcıda ileri ve geri düğmelerini uygulamak için kullanılır.

3. Yığınlar

A Yığın Aşağıdakileri takip eden bir Doğrusal Veri Yapısıdır LİFO (Son Giren, İlk Çıkar) ilkesi, Yığın'ın bir ucundan, yani Üstten ekleme ve silme gibi işlemlere izin verir. Yığınlar, bitişik bellek, bir Dizi ve bitişik olmayan bellek, bir Bağlantılı Liste yardımıyla uygulanabilir. Yığınların gerçek hayattaki örnekleri kitap yığınları, kart desteleri, para yığınları ve çok daha fazlasıdır.

Şekil 5. Gerçek Hayattan Bir Stack Örneği

Yukarıdaki şekil, yeni kitapların Yığın'ın üstüne eklenmesi ve çıkarılması gibi işlemlerin yalnızca bir uçtan gerçekleştirildiği bir Yığın'ın gerçek hayattaki örneğini temsil etmektedir. Yığına ekleme ve silme işleminin yalnızca Yığın'ın üst kısmından yapılabileceği anlamına gelir. Herhangi bir zamanda yalnızca Stack'in üst kısımlarına erişebiliriz.

Yığındaki birincil işlemler aşağıdaki gibidir:

İtmek:Yığına yeni bir öğe ekleme işlemine İtme İşlemi denir.Pop:Yığından öğeleri kaldırma veya silme işlemine Pop İşlemi denir.

Şekil 6. Yığın

Yığınların Bazı Uygulamaları:

1. Yığın, özyinelemeli işlemler için Geçici Depolama Yapısı olarak kullanılır.
2. Yığın ayrıca işlev çağrıları, iç içe geçmiş işlemler ve ertelenen/ertelenen işlevler için Yardımcı Depolama Yapısı olarak da kullanılır.
3. Stacks'ı kullanarak işlev çağrılarını yönetebiliriz.
4. Farklı programlama dillerindeki aritmetik ifadeleri değerlendirmek için yığınlardan da yararlanılır.
5. Yığınlar aynı zamanda iç ek ifadelerini son ek ifadelerine dönüştürmede de faydalıdır.
6. Yığınlar, programlama ortamında ifadenin sözdizimini kontrol etmemizi sağlar.
7. Yığınları kullanarak parantezleri eşleştirebiliriz.
8. Yığınlar bir String'i tersine çevirmek için kullanılabilir.
9. Yığınlar, geri izlemeye dayalı sorunların çözümünde yardımcı olur.
10. Yığınları grafik ve ağaç geçişinde derinlemesine öncelikli aramada kullanabiliriz.
11. Yığınlar ayrıca İşletim Sistemi işlevlerinde de kullanılır.
12. Yığınlar aynı zamanda bir düzenlemedeki GERİ AL ve YENİLE işlevlerinde de kullanılır.

4. Kuyruklar

A Sıra öğelerin eklenmesi ve silinmesiyle ilgili bazı sınırlamalar içeren Yığına benzer doğrusal bir veri yapısıdır. Bir Kuyruğa bir öğenin eklenmesi bir uçta yapılır ve çıkarma diğer uçta veya karşı uçta yapılır. Böylece Kuyruk veri yapısının, veri öğelerini işlemek için FIFO (İlk Giren İlk Çıkar) prensibini takip ettiği sonucuna varabiliriz. Kuyrukların uygulanması Diziler, Bağlantılı Listeler veya Yığınlar kullanılarak yapılabilir. Kuyrukların gerçek hayattaki bazı örnekleri arasında bilet gişesindeki kuyruk, yürüyen merdiven, araba yıkama yeri ve çok daha fazlası yer alır.

Şekil 7. Gerçek Hayattan Bir Kuyruk Örneği

dize karşılaştırması

Yukarıdaki resim, ilk gelen müşteriye her zaman ilk hizmetin verildiği Sırayı anlamamıza yardımcı olabilecek bir sinema bileti gişesinin gerçek hayattaki bir örneğidir. Son gelen müşteriye şüphesiz en son hizmet verilecektir. Kuyruğun her iki ucu da açıktır ve farklı işlemleri yürütebilir. Başka bir örnek, müşterinin istediği hizmeti verdikten sonra ön uçtan çıkarıldığı, müşterinin arka uçtan yerleştirildiği yemek alanı hattıdır.

Kuyruğun birincil işlemleri şunlardır:

Sıraya almak:Bazı veri elemanlarının Kuyruğa eklenmesi veya eklenmesine Enqueue adı verilir. Eleman yerleştirme her zaman arka işaretçinin yardımıyla yapılır.Kuyruktan çıkarma:Veri öğelerinin Kuyruktan silinmesine veya kaldırılmasına Kuyruktan Çıkarma adı verilir. Elemanın silinmesi her zaman ön işaretçinin yardımıyla yapılır.

Şekil 8. Sıra

Kuyrukların Bazı Uygulamaları:

1. Grafiklerde genişlik arama işleminde genellikle kuyruklar kullanılır.
2. Kuyruklar ayrıca, kullanıcılar tarafından basılan tuşları depolamak için bir klavye arabellek kuyruğu ve yazıcı tarafından yazdırılan belgeleri depolamak için bir yazdırma arabellek kuyruğu gibi, İşletim Sistemlerinin İş Zamanlayıcı İşlemlerinde de kullanılır.
3. Kuyruklar CPU planlamasından, İş planlamasından ve Disk Planlamasından sorumludur.
4. Öncelik Kuyrukları, bir tarayıcıdaki dosya indirme işlemlerinde kullanılır.
5. Kuyruklar ayrıca çevresel aygıtlar ile CPU arasında veri aktarımı için de kullanılır.
6. Kuyruklar ayrıca CPU için Kullanıcı Uygulamaları tarafından oluşturulan kesintilerin yönetilmesinden de sorumludur.

Doğrusal Olmayan Veri Yapıları

Doğrusal Olmayan Veri Yapıları, veri öğelerinin sıralı olarak düzenlenmediği veri yapılarıdır. Burada verilerin eklenmesi ve çıkarılması doğrusal bir şekilde mümkün değildir. Bireysel veri öğeleri arasında hiyerarşik bir ilişki vardır.

Doğrusal Olmayan Veri Yapılarının Türleri

Aşağıda genel olarak kullandığımız Doğrusal Olmayan Veri Yapılarının listesi yer almaktadır:

1. Ağaçlar

Ağaç, Doğrusal Olmayan bir Veri Yapısı ve ağacın her düğümünün bir değer ve diğer düğümlere ('çocuklar') referansların bir listesini depolayacağı şekilde bir düğüm koleksiyonu içeren bir hiyerarşidir.

Ağaç veri yapısı, bilgisayardaki verileri daha etkin kullanılacak şekilde düzenlemek ve toplamak için özel bir yöntemdir. Merkezi bir düğüm, yapısal düğümler ve kenarlar aracılığıyla bağlanan alt düğümler içerir. Ağaç veri yapısının birbirine bağlı kökler, dallar ve yapraklardan oluştuğunu da söyleyebiliriz.

Şekil 9. Bir ağaç

Ağaçlar farklı türlere ayrılabilir:

İkili ağaç:Her ana düğümün en fazla iki çocuğa sahip olabileceği Ağaç veri yapısına İkili Ağaç adı verilir.İkili Arama Ağacı:İkili Arama Ağacı, sayıların sıralanmış bir listesini kolayca tutabildiğimiz bir Ağaç veri yapısıdır.AVL Ağacı:AVL Ağacı, her düğümün, değeri -1, 0 veya +1 olan Denge Faktörü olarak bilinen ekstra bilgileri koruduğu, kendi kendini dengeleyen bir İkili Arama Ağacıdır.B-Ağaç:B-Tree, her düğümün birden fazla anahtardan oluştuğu ve ikiden fazla çocuğa sahip olabildiği, kendi kendini dengeleyen özel bir İkili Arama Ağacı türüdür.

Ağaçların Bazı Uygulamaları:

1. Ağaçlar, dizinler ve dosya sistemleri gibi bilgisayar sistemlerinde hiyerarşik yapıları uygular.
2. Ağaçlar ayrıca bir web sitesinin gezinme yapısını uygulamak için de kullanılır.
3. Trees'i kullanarak Huffman'ın koduna benzer kodlar üretebiliriz.
4. Ağaçlar aynı zamanda Oyun uygulamalarında karar vermede de faydalıdır.
5. Ağaçlar, önceliğe dayalı işletim sistemi planlama işlevleri için öncelik sıralarının uygulanmasından sorumludur.
6. Ağaçlar ayrıca farklı programlama dillerinin derleyicilerindeki ifadelerin ve ifadelerin ayrıştırılmasından da sorumludur.
7. Veri Tabanı Yönetim Sistemi (DBMS) için indeksleme amacıyla veri anahtarlarını depolamak için Trees'i kullanabiliriz.
8. Spanning Trees, Bilgisayar ve İletişim Ağlarındaki kararları yönlendirmemize olanak tanır.
9. Ağaçlar aynı zamanda Yapay Zeka (AI), Robotik ve Video Oyunları Uygulamalarında uygulanan yol bulma algoritmasında da kullanılmaktadır.

2. Grafikler

Grafik, sınırlı sayıda düğüm veya köşe ve bunları birbirine bağlayan kenarlardan oluşan Doğrusal Olmayan Veri Yapısının başka bir örneğidir. Grafikler, sorun alanını sosyal ağlar, devre ağları ve telefon ağları gibi bir ağ olarak gösterdiği gerçek dünyanın sorunlarını çözmek için kullanılır. Örneğin, bir Grafiğin düğümleri veya köşeleri bir telefon ağındaki tek bir kullanıcıyı temsil ederken, kenarlar da aralarında telefon yoluyla olan bağlantıyı temsil eder.

Grafik veri yapısı G, aşağıda gösterildiği gibi bir dizi köşeden (V) ve bir dizi kenardan (E) oluşan matematiksel bir yapı olarak kabul edilir:

G = (V,E)

Şekil 10. Grafik

Yukarıdaki şekil yedi köşesi A, B, C, D, E, F, G ve on kenarı [A, B], [A, C], [B, C], [B, D] olan bir Grafiği temsil etmektedir. [B, E], [C, D], [D, E], [D, F], [E, F] ve [E, G].

Köşelerin ve kenarların konumuna bağlı olarak Grafikler farklı tiplere ayrılabilir:

Boş Grafik:Boş bir kenar kümesine sahip bir Grafik, Boş Grafik olarak adlandırılır.Önemsiz Grafik:Yalnızca bir köşeye sahip bir Grafik, Önemsiz Grafik olarak adlandırılır.Basit Grafik:Kendi kendine döngüleri olmayan veya birden fazla kenarı olmayan bir Grafik, Basit Grafik olarak bilinir.Çoklu Grafik:Bir Grafın birden çok kenardan oluşması ancak kendi kendine döngü içermemesi durumunda Çoklu olduğu söylenir.Sözde Grafik:Kendi kendine döngülere ve birden fazla kenara sahip bir Grafik, Pseudo Graph olarak adlandırılır.Yönlendirilmemiş Grafik:Yönlendirilmemiş kenarlardan oluşan bir Grafik, Yönlendirilmemiş Grafik olarak bilinir.Yönlendirilmiş grafik:Köşeler arasındaki yönlendirilmiş kenarlardan oluşan bir Graf, Yönlendirilmiş Grafik olarak bilinir.Bağlı Grafik:Her köşe çifti arasında en az tek bir yol bulunan bir Grafik, Bağlantılı Grafik olarak adlandırılır.Bağlantısız Grafik:En az bir çift köşe arasında herhangi bir yolun bulunmadığı bir Grafik, Bağlantısız Grafik olarak adlandırılır.Düzenli Grafik:Tüm köşelerin aynı dereceye sahip olduğu graflara düzenli graf denir.Grafiğin Tamamı:Tüm köşelerin her köşe çifti arasında bir kenara sahip olduğu bir Grafik, Tam Grafik olarak bilinir.Döngü Grafiği:Bir Grafın, bir döngü oluşturan en az üç köşesi ve kenarı varsa Döngü olduğu söylenir.Döngüsel Grafik:Bir Grafın Döngüsel olduğu ancak ve ancak en az bir döngünün mevcut olduğu söylenir.Döngüsel Olmayan Grafik:Sıfır döngüye sahip bir Grafik, Döngüsel Olmayan Grafik olarak adlandırılır.Sonlu Grafik:Sonlu sayıda köşe ve kenara sahip bir Grafik, Sonlu Grafik olarak bilinir.Sonsuz Grafik:Sonsuz sayıda köşe ve kenara sahip bir Grafik, Sonsuz Grafik olarak bilinir.İki Parçalı Grafik:Köşelerin bağımsız A ve B kümelerine bölünebildiği ve A kümesinin tüm köşelerinin yalnızca bazı kenarları olan B kümesindeki köşelere bağlanması gereken bir Grafik, İki Parçalı Grafik olarak adlandırılır.Düzlemsel Grafik:Bir Graf, iki kenarı birbiriyle kesişen tek bir düzlemde çizilebiliyorsa buna Düzlemsel denir.Euler Grafiği:Bir Grafın Euler olduğu ancak ve ancak tüm köşelerin çift derece olması durumunda söylenir.Hamilton Grafiği:Hamilton devresinden oluşan Bağlantılı Grafik, Hamilton Grafiği olarak bilinir.

Grafiklerin Bazı Uygulamaları:

1. Grafikler ulaşım, seyahat ve iletişim uygulamalarında rotaları ve ağları temsil etmemize yardımcı olur.
2. Grafikler GPS'deki rotaları görüntülemek için kullanılır.
3. Grafikler ayrıca sosyal ağlardaki ve diğer ağ tabanlı uygulamalardaki ara bağlantıları temsil etmemize de yardımcı olur.
4. Haritalama uygulamalarında grafiklerden yararlanılır.
5. Grafikler, e-ticaret uygulamalarında kullanıcı tercihinin temsilinden sorumludur.
6. Grafikler aynı zamanda yerel veya belediye şirketlerinin karşılaştığı sorunları tanımlamak için Hizmet ağlarında da kullanılır.
7. Grafikler aynı zamanda bir kuruluştaki kaynakların kullanımını ve kullanılabilirliğini yönetmeye de yardımcı olur.
8. Grafikler ayrıca, sayfalar arasındaki bağlantıyı köprüler aracılığıyla görüntülemek amacıyla web sitelerinin belge bağlantı haritalarını oluşturmak için de kullanılır.
9. Grafikler aynı zamanda robotik hareketlerde ve sinir ağlarında da kullanılır.

Veri Yapılarının Temel İşlemleri

Aşağıdaki bölümde her veri yapısındaki verileri işlemek için gerçekleştirebileceğimiz farklı işlem türlerini tartışacağız:

Geçiş:Bir veri yapısından geçmek, yönetilebilmesi için her veri öğesine tam olarak bir kez erişilmesi anlamına gelir. Örneğin bir departmandaki tüm çalışanların isimleri yazdırılırken çapraz geçiş yapılması gerekir.Aramak:Arama, belirli kısıtlamaları karşılayan bir veya daha fazla veri öğesinin konumunu bulmak anlamına gelen başka bir veri yapısı işlemidir. Böyle bir veri öğesi, verilen veri öğeleri kümesinde mevcut olabilir veya olmayabilir. Örneğin 5 yıldan fazla tecrübeye sahip tüm çalışanların isimlerini bulmak için arama operasyonunu kullanabiliriz.Ekleme:Ekleme, koleksiyona yeni veri öğeleri eklemek veya eklemek anlamına gelir. Örneğin, şirketin yakın zamanda işe aldığı yeni bir çalışanın ayrıntılarını eklemek için ekleme işlemini kullanabiliriz.Silme:Silme, belirli bir veri öğesini verilen veri öğeleri listesinden kaldırmak veya silmek anlamına gelir. Örneğin işten ayrılan bir çalışanın ismini silmek için silme işlemini kullanabiliriz.Sıralama:Sıralama, uygulama türüne bağlı olarak veri öğelerini Artan veya Azalan düzende düzenlemek anlamına gelir. Örneğin, bir departmandaki çalışanların adlarını alfabetik sıraya göre düzenlemek için sıralama işlemini kullanabiliriz veya çalışanların performansını azalan düzende düzenleyip ilk üçün ayrıntılarını çıkararak ayın en iyi üç performansını tahmin etmek için kullanabiliriz.Birleştirmek:Birleştirme, sıralanmış veri öğelerinin tek bir listesini oluşturmak için iki sıralı listenin veri öğelerini birleştirmek anlamına gelir.Yaratmak:Create, programın veri elemanlarına hafıza ayırmak için kullanılan bir işlemdir. Bu işlemi bir bildirim ifadesi kullanarak gerçekleştirebiliriz. Veri yapısının oluşturulması aşağıdakilerden herhangi biri sırasında gerçekleşebilir:
1. Derleme zamanı
2. Çalışma süresi
   Örneğin, malloc() C dilinde veri yapısını oluşturmak için fonksiyon kullanılır.
Seçim:Seçim, mevcut verilerden belirli bir verinin seçilmesi anlamına gelir. Döngü içindeki koşulları belirterek herhangi bir veriyi seçebiliriz.Güncelleme:Güncelleme işlemi veri yapısındaki verileri güncellememizi veya değiştirmemizi sağlar. Ayrıca Seçim işlemi gibi döngü içindeki bazı koşulları belirterek herhangi bir veriyi güncelleyebiliriz.Bölme:Bölme işlemi, verileri çeşitli alt bölümlere ayırmamıza olanak tanır ve genel işlem tamamlanma süresini azaltır.

Soyut Veri Türünü Anlamak

Göre Ulusal Standartlar ve Teknoloji Enstitüsü (NIST) Veri yapısı, daha iyi algoritma verimliliği için genellikle bellekte bulunan bilgilerin bir düzenlemesidir. Veri Yapıları bağlantılı listeleri, yığınları, kuyrukları, ağaçları ve sözlükleri içerir. Bir kişinin adı ve adresi gibi teorik bir varlık da olabilirler.

Yukarıda bahsedilen tanımdan veri yapısındaki işlemlerin şunları içerdiği sonucuna varabiliriz:

gazoz java

1. Bir listeden bir öğenin eklenmesi veya silinmesi gibi yüksek düzeyde soyutlamalar.
2. Listedeki bir öğeyi arama ve sıralama.
3. Bir listedeki en yüksek öncelikli öğeye erişim.

Veri yapısı bu tür işlemleri her yaptığında buna denir. Soyut Veri Türü (ADT) .

Veriler üzerinde yapılan işlemlerle birlikte veri elemanları kümesi olarak tanımlayabiliriz. 'Soyut' terimi, verilerin ve üzerinde tanımlanan temel işlemlerin, uygulamalarından bağımsız olarak incelendiği anlamına gelir. Nasıl yapabileceğimizi değil, verilerle ne yapabileceğimizi içerir.

Bir ADI uygulaması, temel işlemler için veri öğelerini ve algoritmaları depolamak amacıyla bir depolama yapısı içerir. Dizi, bağlantılı liste, kuyruk, yığın vb. gibi tüm veri yapıları ADT örnekleridir.

ADT Kullanmanın Avantajlarını Anlamak

Gerçek dünyada programlar yeni kısıtlamaların veya gereksinimlerin bir sonucu olarak gelişir, dolayısıyla bir programı değiştirmek genellikle bir veya daha fazla veri yapısında değişiklik yapılmasını gerektirir. Örneğin, her çalışan hakkında daha fazla ayrıntıyı takip etmek için bir çalışanın kaydına yeni bir alan eklemek istediğimizi varsayalım. Bu durumda Array'i Linked yapıyla değiştirerek programın verimliliğini artırabiliriz. Böyle bir durumda, değiştirilmiş yapıyı kullanan her prosedürün yeniden yazılması uygun değildir. Bu nedenle daha iyi bir alternatif, bir veri yapısını uygulama bilgilerinden ayırmaktır. Soyut Veri Türlerinin (ADT) kullanımının ardındaki prensip budur.

Veri Yapılarının Bazı Uygulamaları

Aşağıda Veri Yapılarının bazı uygulamaları verilmiştir:

1. Veri Yapıları, bilgisayarın belleğindeki verilerin düzenlenmesine yardımcı olur.
2. Veri Yapıları ayrıca veritabanlarındaki bilgilerin temsil edilmesine de yardımcı olur.
3. Veri Yapıları, verilerde arama yapmak için algoritmaların uygulanmasına olanak tanır (Örneğin, arama motoru).
4. Verileri işlemeye yönelik algoritmaları uygulamak için Veri Yapılarını kullanabiliriz (Örneğin, kelime işlemciler).
5. Veri Yapılarını (Örneğin veri madencileri) kullanarak verileri analiz etmek için algoritmalar da uygulayabiliriz.
6. Veri Yapıları, verileri oluşturmak için algoritmaları destekler (Örneğin, rastgele sayı üreteci).
7. Veri Yapıları ayrıca verileri sıkıştırmaya ve sıkıştırmayı açmaya yönelik algoritmaları da destekler (Örneğin, bir zip yardımcı programı).
8. Verileri şifrelemek ve şifresini çözmek için algoritmalar uygulamak için Veri Yapılarını da kullanabiliriz (Örneğin, bir güvenlik sistemi).
9. Veri Yapıları'nın yardımıyla dosyaları ve dizinleri yönetebilen yazılımlar (Örneğin, bir dosya yöneticisi) geliştirebiliriz.
10. Veri Yapılarını kullanarak grafikleri oluşturabilen yazılımlar da geliştirebiliriz. (Örneğin, bir web tarayıcısı veya 3D oluşturma yazılımı).

Bunların dışında, daha önce de belirtildiği gibi, Veri Yapılarının istenen herhangi bir yazılımı oluşturmamıza yardımcı olabilecek başka birçok uygulaması vardır.