Bu yazımızda veri yapısında ağaç geçişini ele alacağız. 'Ağaç geçişi' terimi, bir ağacın her bir düğümünü geçmek veya ziyaret etmek anlamına gelir. Bağlantılı liste, kuyruk ve yığın gibi doğrusal veri yapısında geçiş yapmanın tek bir yolu vardır. Oysa bir ağacı geçmenin aşağıda sıralanan birden fazla yolu vardır:
- Ön sipariş geçişi
- Sıralı geçiş
- Posta siparişi geçişi
Bu nedenle, bu makalede yukarıda sıralanan ağaçta gezinme tekniklerini tartışacağız. Şimdi ağaç geçiş yollarını tartışmaya başlayalım.
Ön sipariş geçişi
Bu teknik 'kök sol sağ' politikasını izler. Bu, ilk kök düğümün ziyaret edilmesi, ardından sol alt ağacın yinelemeli olarak geçilmesi ve son olarak sağ alt ağacın yinelemeli olarak geçilmesi anlamına gelir. Kök düğüm sol ve sağ alt ağaçtan önce (veya öncesinde) geçildiği için buna ön sıra geçişi denir.
Yani, bir ön sipariş geçişinde her düğüm, her iki alt ağacından önce ziyaret edilir.
Ön sipariş geçişinin uygulamaları şunları içerir:
- Ağacın bir kopyasını oluşturmak için kullanılır.
- Bir ifade ağacının önek ifadesini elde etmek için de kullanılabilir.
Algoritma
Until all nodes of the tree are not visited Step 1 - Visit the root node Step 2 - Traverse the left subtree recursively. Step 3 - Traverse the right subtree recursively.
Örnek
Şimdi ön sipariş geçiş tekniği örneğini görelim.
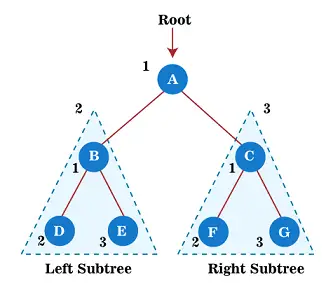
Şimdi yukarıdaki ağaçta ön sipariş geçişini uygulamaya başlayın. İlk önce kök düğümü geçiyoruz A; bundan sonra sol alt ağacına gidin B , bu da ön siparişte geçilecek.
Yani, sol alt ağaç B için ilk olarak kök düğüm B kendisi geçilir; bundan sonra sol alt ağacı D geçilir. Düğümden beri D hiç çocuğu yok, sağ alt ağaca git VE . E düğümünün de çocuğu olmadığından, A kök düğümünün sol alt ağacının geçişi tamamlanır.
piton yol ayarı
Şimdi, A kök düğümünün sağ alt ağacı olan C'ye doğru ilerleyin. Yani, sağ C alt ağacı için önce kök düğüm C kendi içinden geçti; bundan sonra sol alt ağacı F geçilir. Düğümden beri F hiç çocuğu yok, sağ alt ağaca git G . G düğümünün de çocuğu olmadığından, A kök düğümünün sağ alt ağacının çapraz geçişi tamamlanır.
Bu nedenle ağacın tüm düğümleri geçilir. Yani yukarıdaki ağacın ön sipariş geçişinin çıktısı:
bahar önyükleme ek açıklamaları
A → B → D → E → C → F → G
Veri yapısında ön sipariş geçişi hakkında daha fazla bilgi edinmek için bağlantıyı takip edebilirsiniz. Ön sipariş geçişi .
Posta siparişi geçişi
Bu teknik 'sol-sağ kök' politikasını izler. Bu, kök düğümün ilk sol alt ağacının geçildiği, ardından yinelemeli olarak sağ alt ağacın geçildiği ve son olarak kök düğümün geçildiği anlamına gelir. Kök düğüm sol ve sağ alt ağaçtan sonra (veya sonra) geçildiği için buna postorder geçişi denir.
Dolayısıyla, bir sipariş sonrası geçişte her düğüm, her iki alt ağacından sonra ziyaret edilir.
Sipariş sonrası geçiş uygulamaları şunları içerir:
- Ağacı silmek için kullanılır.
- Bir ifade ağacının son ek ifadesini elde etmek için de kullanılabilir.
Algoritma
Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Traverse the right subtree recursively. Step 3 - Visit the root node.
Örnek
Şimdi sipariş sonrası geçiş tekniği örneğini görelim.

Şimdi yukarıdaki ağaçta postorder geçişini uygulamaya başlayın. İlk önce, sonradan geçilecek olan sol alt ağaç B'yi geçiyoruz. Bundan sonra sağ alt ağaçtan geçeceğiz C posta siparişinde. Ve son olarak yukarıdaki ağacın kök düğümü, yani A , geçilir.
Yani, sol alt ağaç B için, önce sol alt ağacı D geçilir. Düğümden beri D hiç çocuğu yok, sağ alt ağacı geç VE . E düğümünün de çocuğu olmadığından kök düğüme geçin B. Düğümü geçtikten sonra B, A kök düğümünün sol alt ağacının geçişi tamamlanır.
Şimdi, kök düğüm A'nın sağ alt ağacı olan C'ye doğru ilerleyin. Yani, sağ C alt ağacı için önce onun sol alt ağacı F geçilir. Düğümden beri F hiç çocuğu yok, sağ alt ağacı geç G . G düğümünün de çocuğu olmadığından, son olarak sağ alt ağacın kök düğümü, yani, C, geçilir. A kök düğümünün sağ alt ağacının geçişi tamamlandı.
oyuncu Zeenat Aman
Sonunda belirli bir ağacın kök düğümünü geçin, yani: A . Kök düğümü geçtikten sonra, verilen ağacın postorder geçişi tamamlanır.
Bu nedenle ağacın tüm düğümleri geçilir. Yani, yukarıdaki ağacın postorder geçişinin çıktısı şu şekildedir:
D → E → B → F → G → C → A
Veri yapısında postorder geçişi hakkında daha fazla bilgi edinmek için bağlantıyı takip edebilirsiniz. Posta siparişi geçişi .
Sıralı geçiş
Bu teknik 'sol kök sağ' politikasını izler. Bu, kök düğüm geçildikten sonra ilk sol alt ağacın ziyaret edildiği ve son olarak sağ alt ağacın geçildiği anlamına gelir. Kök düğüm sol ve sağ alt ağaç arasında gezindiğinden, sırayla geçiş olarak adlandırılır.
Yani sıralı geçişte her düğüm kendi alt ağaçları arasında ziyaret edilir.
Inorder geçişinin uygulamaları şunları içerir:
- BST düğümlerini artan sırada elde etmek için kullanılır.
- Bir ifade ağacının önek ifadesini elde etmek için de kullanılabilir.
Algoritma
Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Visit the root node. Step 3 - Traverse the right subtree recursively.
Örnek
haritayı parçala
Şimdi Inorder geçiş tekniği örneğini görelim.

Şimdi yukarıdaki ağaçta sıralı geçişi uygulamaya başlayın. İlk önce sol alt ağaçtan geçiyoruz B bu sırayla geçilecektir. Bundan sonra kök düğümü geçeceğiz A . Ve son olarak sağ alt ağaç C sırayla geçilir.
Yani sol alt ağaç için B , ilk olarak sol alt ağacı D geçilir. Düğümden beri D hiç çocuğu yok, bu yüzden onu geçtikten sonra düğüm B geçilecek ve sonunda B düğümünün sağ alt ağacı, yani VE , geçilir. Düğüm E'nin de çocuğu yoktur; bu nedenle A kök düğümünün sol alt ağacının geçişi tamamlanır.
Bundan sonra belirli bir ağacın kök düğümünü geçin; A .
Son olarak, kök düğüm A'nın sağ alt ağacı olan C'ye doğru ilerleyin. Yani, sağ C alt ağacı için; ilk olarak sol alt ağacı F geçilir. Düğümden beri F hiç çocuğu yok, düğüm C geçilecek ve sonunda C düğümünün sağ alt ağacı, yani, G , geçilir. Düğüm G'nin de çocuğu yoktur; bu nedenle A kök düğümünün sağ alt ağacının geçişi tamamlanır.
Ağacın tüm düğümleri geçildiğinden, söz konusu ağacın sıralı geçişi tamamlanır. Yukarıdaki ağacın sıralı geçişinin çıktısı:
D → B → E → A → F → C → G
Veri yapısındaki sıralı geçiş hakkında daha fazla bilgi edinmek için bağlantıyı takip edebilirsiniz. Sıralı Geçiş .
Ağaç geçiş tekniklerinin karmaşıklığı
Yukarıda tartışılan ağaç geçiş tekniklerinin zaman karmaşıklığı Açık) , Neresi 'N' ikili ağacın boyutudur.
yazı tipi
Yukarıda tartışılan ağaç geçiş tekniklerinin uzay karmaşıklığı Ç(1) işlev çağrıları için yığın boyutunu dikkate almazsak. Aksi takdirde, bu tekniklerin uzay karmaşıklığı Ah) , Neresi 'H' ağacın yüksekliğidir.
Ağaç geçişinin uygulanması
Şimdi yukarıda tartışılan tekniklerin farklı programlama dilleri kullanılarak uygulanmasını görelim.
Program: C'de ağaç geçiş tekniklerini uygulayan bir program yazın.
#include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; printf(' %d ', root->element); traversePreorder(root->left); traversePreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); printf(' %d ', root->element); traverseInorder(root->right); } /*function to traverse the nodes of binary tree in postorder*/ void traversePostorder(struct node* root) { if (root == NULL) return; traversePostorder(root->left); traversePostorder(root->right); printf(' %d ', root->element); } int main() { struct node* root = createNode(36); root->left = createNode(26); root->right = createNode(46); root->left->left = createNode(21); root->left->right = createNode(31); root->left->left->left = createNode(11); root->left->left->right = createNode(24); root->right->left = createNode(41); root->right->right = createNode(56); root->right->right->left = createNode(51); root->right->right->right = createNode(66); printf('
The Preorder traversal of given binary tree is -
'); traversePreorder(root); printf('
The Inorder traversal of given binary tree is -
'); traverseInorder(root); printf('
The Postorder traversal of given binary tree is -
'); traversePostorder(root); return 0; } Çıktı

Program: C#'ta ağaç geçiş tekniklerini uygulayan bir program yazın.
using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traversePreorder(Node node) { if (node == null) return; Console.Write(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); Console.Write(node.value + ' '); traverseInorder(node.right); } void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); Console.Write(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(37); bt.root.left = new Node(27); bt.root.right = new Node(47); bt.root.left.left = new Node(22); bt.root.left.right = new Node(32); bt.root.left.left.left = new Node(12); bt.root.left.left.right = new Node(25); bt.root.right.left = new Node(42); bt.root.right.right = new Node(57); bt.root.right.right.left = new Node(52); bt.root.right.right.right = new Node(67); Console.WriteLine('The Preorder traversal of given binary tree is - '); bt.traversePreorder(); Console.WriteLine(); Console.WriteLine('The Inorder traversal of given binary tree is - '); bt.traverseInorder(); Console.WriteLine(); Console.WriteLine('The Postorder traversal of given binary tree is - '); bt.traversePostorder(); } } Çıktı

Program: C++'da ağaç geçiş tekniklerini uygulayan bir program yazın.
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; cout<<' '<element<left); traversepreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); cout<<' '<element<right); } *function to traverse the nodes of binary tree in postorder* void traversepostorder(struct node* root) { if (root="=" null) return; traversepostorder(root->left); traversePostorder(root->right); cout<<' '<element<left="createNode(28);" root->right = createNode(48); root->left->left = createNode(23); root->left->right = createNode(33); root->left->left->left = createNode(13); root->left->left->right = createNode(26); root->right->left = createNode(43); root->right->right = createNode(58); root->right->right->left = createNode(53); root->right->right->right = createNode(68); cout<<'
the preorder traversal of given binary tree is -
'; traversepreorder(root); cout<<'
inorder traverseinorder(root); postorder traversepostorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-6.webp" alt="Tree Traversal"> <p> <strong>Program:</strong> Write a program to implement tree traversal techniques in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class Tree { Node root; /* root of the tree */ Tree() { root = null; } /*function to print the nodes of given binary in Preorder*/ void traversePreorder(Node node) { if (node == null) return; System.out.print(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } /*function to print the nodes of given binary in Inorder*/ void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } /*function to print the nodes of given binary in Postorder*/ void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); System.out.print(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } public static void main(String args[]) { Tree pt = new Tree(); pt.root = new Node(36); pt.root.left = new Node(26); pt.root.right = new Node(46); pt.root.left.left = new Node(21); pt.root.left.right = new Node(31); pt.root.left.left.left = new Node(11); pt.root.left.left.right = new Node(24); pt.root.right.left = new Node(41); pt.root.right.right = new Node(56); pt.root.right.right.left = new Node(51); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Preorder traversal of given binary tree is - '); pt.traversePreorder(); System.out.println('
'); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println('
'); System.out.println('The Postorder traversal of given binary tree is - '); pt.traversePostorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-7.webp" alt="Tree Traversal"> <h2>Conclusion</h2> <p>In this article, we have discussed the different types of tree traversal techniques: preorder traversal, inorder traversal, and postorder traversal. We have seen these techniques along with algorithm, example, complexity, and implementation in C, C++, C#, and java.</p> <p>So, that's all about the article. Hope it will be helpful and informative to you.</p> <hr></'
></'></'></'> Çıktı
Yukarıdaki kodun yürütülmesinden sonra çıktı şu şekilde olacaktır:

Çözüm
Bu makalede, farklı ağaç geçişi tekniklerini tartıştık: ön sipariş geçişi, sıralı geçiş ve sipariş sonrası geçiş. Bu teknikleri algoritma, örnek, karmaşıklık ve C, C++, C# ve Java'daki uygulamalarla birlikte gördük.
Yani bu makaleyle ilgili. Umarım sizler için faydalı ve bilgilendirici olur.
