Bu yazımızda veri yapısında sıralı geçiş konusunu ele alacağız.
Düğümleri artan sırada dolaşmak istiyorsak, sıralı geçişi kullanırız. Sıralı geçiş için gerekli adımlar şunlardır:
- Sol alt ağaçtaki tüm düğümleri ziyaret edin
- Kök düğümü ziyaret edin
- Sağ alt ağaçtaki tüm düğümleri ziyaret edin
Yığın, dizi, kuyruk vb. gibi doğrusal veri yapılarının verileri dolaşmak için yalnızca tek bir yolu vardır. Ancak hiyerarşik veri yapılarında ağaç, Verileri geçmenin birden fazla yolu vardır. Burada ağaç veri yapısını geçmenin başka bir yolunu, yani sıralı geçişi tartışacağız.
Sıralı geçiş için kullanılan iki yaklaşım vardır:
- Özyinelemeyi kullanarak sıra geçişi
- Yinelemeli bir yöntem kullanarak sıra geçişi
Sırasız bir geçiş tekniği aşağıdaki gibidir: Sol Kök Sağ politika. Burada Sol Kök Sağ, önce kök düğümün sol alt ağacının geçildiği, ardından kök düğümün ve ardından kök düğümün sağ alt ağacının geçildiği anlamına gelir. Burada, inorder adının kendisi, kök düğümün sol ve sağ alt ağaçların arasına girdiğini göstermektedir.
Hem özyinelemeli hem de yinelemeli teknikleri kullanarak sıralı geçişi tartışacağız. İlk önce özyinelemeyi kullanarak sıralı geçişle başlayalım.
Özyinelemeyi kullanarak sıralı geçiş
Step 1: Recursively traverse the left subtree Step 2: Now, visit the root Step 3: Traverse the right subtree recursively
Sırasız geçiş örneği
Şimdi sırasız geçişin bir örneğini görelim. Bir örnek kullanarak sıralı geçiş prosedürünü anlamak daha kolay olacaktır.
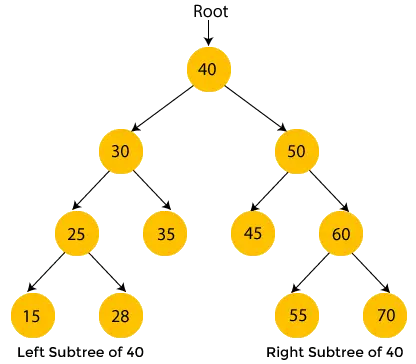
Sarı renkli düğümler henüz ziyaret edilmemiştir. Şimdi yukarıdaki ağacın düğümlerini sıralı geçiş kullanarak geçeceğiz.
- Burada 40 kök düğümdür. 40'ın sol alt ağacına, yani 30'a gidiyoruz ve onun da 25 numaralı alt ağacı var, dolayısıyla tekrar 25'in sol alt ağacına yani 15'e geçiyoruz. Burada 15'in alt ağacı yok, dolayısıyla 15 yazdır ve ana düğümüne (25) doğru ilerleyin.
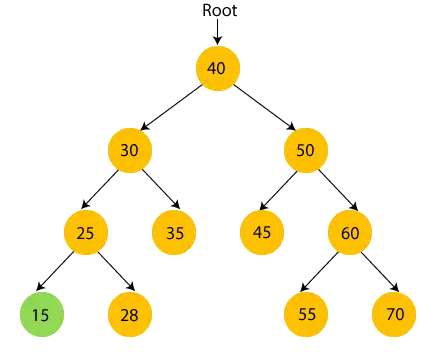
- Şimdi, yazdır 25 ve 25'in sağ alt ağacına gidin.
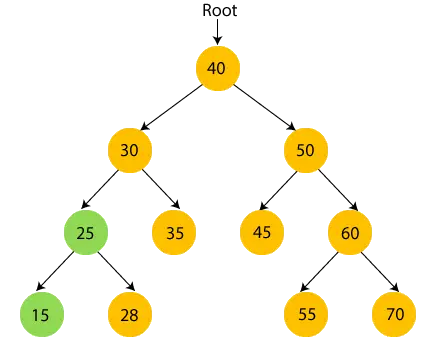
- Şimdi, yazdır 28 ve 25'in kök düğümüne yani 30'a gidin.
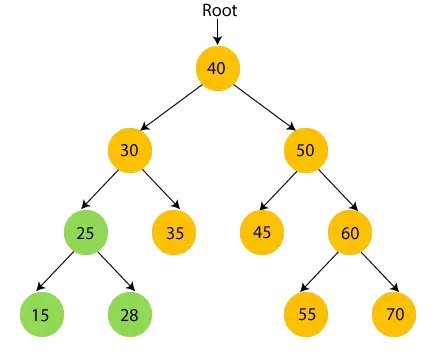
- Böylece 30'un sol alt ağacı ziyaret edilir. Şimdi, 30 yazdır ve 30 yaşındaki sağ çocuğa geçin.
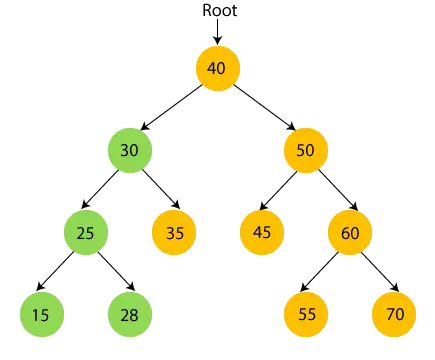
- Şimdi, yazdır 35 ve 30'un kök düğümüne gidin.
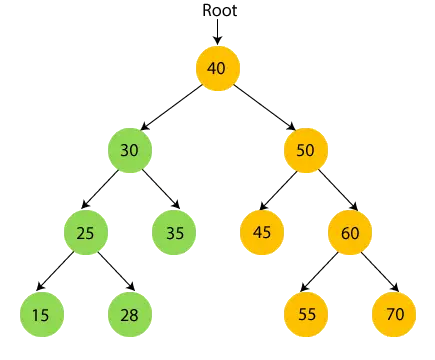
- Şimdi, kök düğüm 40'ı yazdır ve sağ alt ağacına gidin.
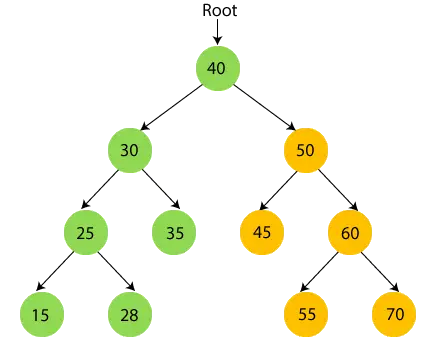
- Şimdi 40'ın sağ alt ağacını yani 50'yi yinelemeli olarak geçelim.
50'nin alt ağacı var, bu yüzden önce 50'nin sol alt ağacını geçin, yani 45. 45'in çocuğu yok, yani baskı 45 ve kök düğümüne gidin.
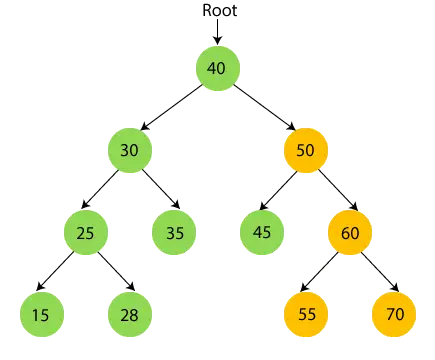
- Şimdi 50 yazdır ve 50'nin sağ alt ağacına, yani 60'a gidin.
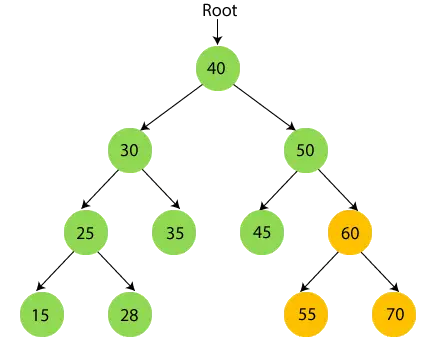
- Şimdi yinelemeli olarak 50'nin sağ alt ağacını, yani 60'ı geçin. 60'ın alt ağacı var, bu nedenle önce 60'ın sol alt ağacını yani 55'i geçin. 55'in çocuğu yok, dolayısıyla yazdır 55 ve kök düğümüne gidin.
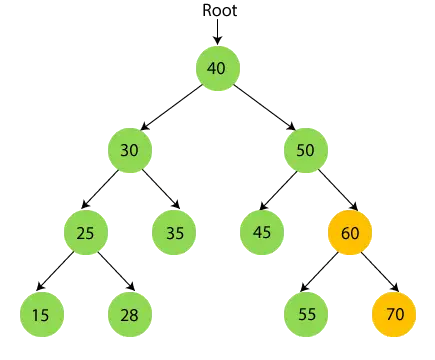
- Şimdi 60 yazdır ve 60'ın sağ alt ağacına, yani 70'e gidin.
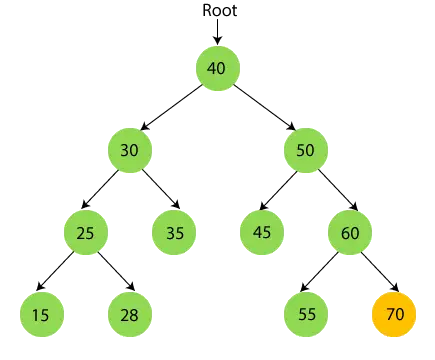
- Şimdi 70 yazdır.
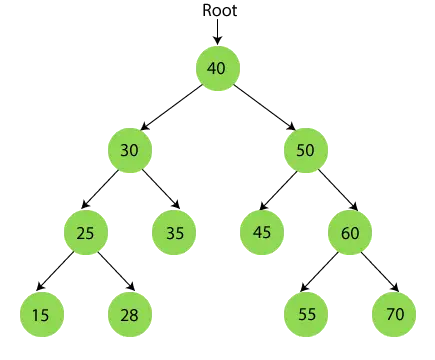
Sıralı geçiş tamamlandıktan sonra nihai çıktı şu şekildedir:
{15, 25, 28, 30, 35, 40, 45, 50, 55, 60, 70}
Sırasız geçişin karmaşıklığı
Sırasız geçişin zaman karmaşıklığı Açık), burada 'n' ikili ağacın boyutudur.
bahar çizme
Oysa sırasız geçişin uzay karmaşıklığı Ç(1), işlev çağrıları için yığın boyutunu dikkate almazsak. Aksi takdirde, sırasız geçişin uzay karmaşıklığı Ah), burada 'h' ağacın yüksekliğidir.
Inorder geçişinin uygulanması
Şimdi farklı programlama dillerinde sıralı geçişin uygulanmasını görelim.
Program: C dilinde sıralı geçiş uygulayacak bir program yazın.
#include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); printf(' %d ', root->element); traverseInorder(root->right); } int main() { struct node* root = createNode(40); root->left = createNode(30); root->right = createNode(50); root->left->left = createNode(25); root->left->right = createNode(35); root->left->left->left = createNode(15); root->left->left->right = createNode(28); root->right->left = createNode(45); root->right->right = createNode(60); root->right->right->left = createNode(55); root->right->right->right = createNode(70); printf('
The Inorder traversal of given binary tree is -
'); traverseInorder(root); return 0; } Çıktı

Program: C++'ta sıralı geçiş uygulayacak bir program yazın.
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); cout<<' '<element<right); } int main() { struct node* root="createNode(39);" root->left = createNode(29); root->right = createNode(49); root->left->left = createNode(24); root->left->right = createNode(34); root->left->left->left = createNode(14); root->left->left->right = createNode(27); root->right->left = createNode(44); root->right->right = createNode(59); root->right->right->left = createNode(54); root->right->right->right = createNode(69); cout<<'
the inorder traversal of given binary tree is -
'; traverseinorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/15/inorder-traversal-14.webp" alt="Inorder Traversal"> <p> <strong>Program:</strong> Write a program to implement inorder traversal in C#.</p> <pre> using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); Console.Write(node.value + ' '); traverseInorder(node.right); } void traverseInorder() { traverseInorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(36); bt.root.left = new Node(26); bt.root.right = new Node(46); bt.root.left.left = new Node(21); bt.root.left.right = new Node(31); bt.root.left.left.left = new Node(11); bt.root.left.left.right = new Node(24); bt.root.right.left = new Node(41); bt.root.right.right = new Node(56); bt.root.right.right.left = new Node(51); bt.root.right.right.right = new Node(66); Console.WriteLine('The Inorder traversal of given binary tree is - '); bt.traverseInorder(); } } </pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/15/inorder-traversal-15.webp" alt="Inorder Traversal"> <p> <strong>Program:</strong> Write a program to implement inorder traversal in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class InorderTraversal { Node root; InorderTraversal() { root = null; } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } void traverseInorder() { traverseInorder(root); } public static void main(String args[]) { InorderTraversal pt = new InorderTraversal(); pt.root = new Node(35); pt.root.left = new Node(25); pt.root.right = new Node(45); pt.root.left.left = new Node(20); pt.root.left.right = new Node(30); pt.root.left.left.left = new Node(10); pt.root.left.left.right = new Node(23); pt.root.right.left = new Node(40); pt.root.right.right = new Node(55); pt.root.right.right.left = new Node(50); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/15/inorder-traversal-16.webp" alt="Inorder Traversal"> <p>So, that's all about the article. Hope the article will be helpful and informative to you.</p> <hr></'
></'> Çıktı

Program: Java'da sıralı geçiş uygulayacak bir program yazın.
class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class InorderTraversal { Node root; InorderTraversal() { root = null; } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } void traverseInorder() { traverseInorder(root); } public static void main(String args[]) { InorderTraversal pt = new InorderTraversal(); pt.root = new Node(35); pt.root.left = new Node(25); pt.root.right = new Node(45); pt.root.left.left = new Node(20); pt.root.left.right = new Node(30); pt.root.left.left.left = new Node(10); pt.root.left.left.right = new Node(23); pt.root.right.left = new Node(40); pt.root.right.right = new Node(55); pt.root.right.right.left = new Node(50); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println(); } } Çıktı

Yani bu makaleyle ilgili. Umarım makale sizin için yararlı ve bilgilendirici olacaktır.











