YEDI SEGMENTLI EKRANDA MINIMUM SEGMENTLER

Sayıları görüntülemek için yedi bölümlü bir ekran kullanılabilir. Bir dizi göz önüne alındığında N doğal sayılar. Görev, sayıyı görüntülemek için minimum sayıda parçayı kullanan dizideki sayıyı bulmaktır. Birden fazla sayının minimum sayıda bölümü varsa, en küçük dizine sahip sayının çıktısı alınır.

Yedi Segmentli Ekran' title=

Örnekler:

Giriş : dizi[] = { 1 2 3 4 5 }.
Çıkış : 1
Açıklama: Minimum segment sayısını kullanan öğe 1'dir (yani 2 segment)
Giriş: dizi[] = { 489 206 745 123 756 }.
Çıkış : 745
Açıklama: Minimum bölüm sayısını kullanan en küçük dizine sahip öğe 745'tir (yani 12 bölüm)

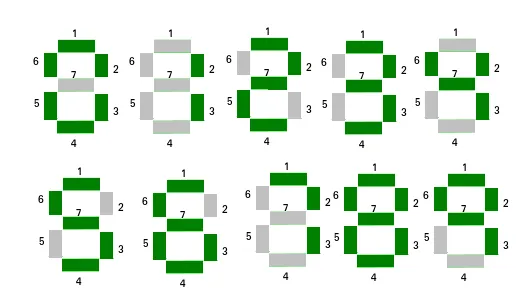
Buradaki fikir, 0'dan 9'a kadar olan rakamların kullandığı segment sayısını önceden hesaplamak ve saklamaktır. Şimdi dizinin her elemanı için, her rakamın kullandığı segment sayısını toplayın. Daha sonra minimum sayıda segment kullanan elemanı bulun.

Rakam tarafından kullanılan segment sayısı:
0 -> 6
1 -> 2
2 -> 5
3 -> 5
4 -> 4
5 -> 5
6 -> 6
7 -> 3
8 -> 7
9 -> 6

C++

#include   using namespace std; // Precomputed values of segment used by digit 0 to 9. const int seg[10] = { 6 2 5 5 4 5 6 3 7 6}; // Return the number of segments used by x. int computeSegment(int x) {  if (x == 0)  return seg[0];  int count = 0;  // Finding sum of the segment used by  // each digit of a number.  while (x)  {  count += seg[x%10];  x /= 10;  }  return count; } int elementMinSegment(vector<int> arr int n) {  // Initialising the minimum segment and minimum  // number index.  int minseg = computeSegment(arr[0]);  int minindex = 0;  // Finding and comparing segment used  // by each number arr[i].  for (int i = 1; i < n; i++)  {  int temp = computeSegment(arr[i]);  // If arr[i] used less segment then update  // minimum segment and minimum number.  if (temp < minseg)  {  minseg = temp;  minindex = i;  }  }  return arr[minindex]; } int main() {  vector<int> arr = {489 206 745 123 756};  int n = arr.size();   cout << elementMinSegment(arr n) << endl;  return 0; }

Java

import java.io.*; class GFG {   // Precomputed values of segment  // used by digit 0 to 9. static int []seg = { 6 2 5 5 4 5 6 3 7 6}; // Return the number of segments used by x. static int computeSegment(int x) {  if (x == 0)  return seg[0];  int count = 0;  // Finding sum of the segment used by  // each digit of a number.  while (x > 0)  {  count += seg[x % 10];  x /= 10;  }  return count; } static int elementMinSegment(int []arr int n) {  // Initialising the minimum segment   // and minimum number index.  int minseg = computeSegment(arr[0]);  int minindex = 0;  // Finding and comparing segment used  // by each number arr[i].  for (int i = 1; i < n; i++)  {  int temp = computeSegment(arr[i]);  // If arr[i] used less segment then update  // minimum segment and minimum number.  if (temp < minseg)  {  minseg = temp;  minindex = i;  }  }  return arr[minindex]; }  static public void main (String[] args)  {  int []arr = {489 206 745 123 756};  int n = arr.length;  System.out.println(elementMinSegment(arr n));  } }

Python

# Precomputed values of segment # used by digit 0 to 9. seg = [6 2 5 5 4 5 6 3 7 6] # Return the number of # segments used by x. def computeSegment(x): if(x == 0): return seg[0] count = 0 # Finding sum of the segment  # used by each digit of a number. while(x): count += seg[x % 10] x = x // 10 return count # function to return minimum sum index def elementMinSegment(arr n): # Initialising the minimum  # segment and minimum number index. minseg = computeSegment(arr[0]) minindex = 0 # Finding and comparing segment # used by each number arr[i]. for i in range(1 n): temp = computeSegment(arr[i]) # If arr[i] used less segment # then update minimum segment # and minimum number. if(temp < minseg): minseg = temp minindex = i return arr[minindex] # Driver Code arr = [489 206 745 123 756] n = len(arr) # function print required answer print(elementMinSegment(arr n)) # This code is contributed by # Sanjit_Prasad

using System; class GFG{   // Precomputed values of segment // used by digit 0 to 9. static int []seg = new int[10]{ 6 2 5 5 4  5 6 3 7 6}; // Return the number of segments used by x. static int computeSegment(int x) {  if (x == 0)  return seg[0];  int count = 0;  // Finding sum of the segment used by  // each digit of a number.  while (x > 0)  {  count += seg[x % 10];  x /= 10;  }  return count; } static int elementMinSegment(int []arr int n) {  // Initialising the minimum segment  // and minimum number index.  int minseg = computeSegment(arr[0]);  int minindex = 0;  // Finding and comparing segment used  // by each number arr[i].  for (int i = 1; i < n; i++)  {  int temp = computeSegment(arr[i]);  // If arr[i] used less segment then update  // minimum segment and minimum number.  if (temp < minseg)  {  minseg = temp;  minindex = i;  }  }  return arr[minindex]; }  static public void Main()  {  int []arr = {489 206 745 123 756};  int n = arr.Length;  Console.WriteLine(elementMinSegment(arr n));  } }

JavaScript

// Precomputed values of segment // used by digit 0 to 9. let seg = [ 6 2 5 5 4 5 6 3 7 6]; // Return the number of segments used by x. function computeSegment(x) {  if (x == 0)  return seg[0];  let count = 0;  // Finding sum of the segment used by  // each digit of a number.  while (x > 0)  {  count += seg[x % 10];  x = parseInt(x / 10 10);  }  return count; } function elementMinSegment(arr n) {    // Initialising the minimum segment  // and minimum number index.  let minseg = computeSegment(arr[0]);  let minindex = 0;  // Finding and comparing segment used  // by each number arr[i].  for(let i = 1; i < n; i++)  {  let temp = computeSegment(arr[i]);  // If arr[i] used less segment then update  // minimum segment and minimum number.  if (temp < minseg)  {  minseg = temp;  minindex = i;  }  }  return arr[minindex]; } // Driver code let arr = [ 489 206 745 123 756 ]; let n = arr.length; console.log(elementMinSegment(arr n));

Çıkış

Zaman Karmaşıklığı: O(n * log ₁₀ N)
Yardımcı Alan: O(10)

Test Oluştur

TechCodeview

Yedi Segmentli Ekranda Minimum Segmentler