• Desenleri tanımak için sonlu durum makinesi kullanılır.
• Sonlu otomata makinesi, sembol dizisini girdi olarak alır ve durumunu buna göre değiştirir. Girişte istenilen sembol bulunduğunda geçiş gerçekleşir.
• Geçiş sırasında otomatlar ya bir sonraki duruma geçebilir ya da aynı durumda kalabilir.
• FA'nın iki durumu vardır: kabul durumu veya reddetme durumu. Giriş dizesi başarılı bir şekilde işlendiğinde ve otomatlar son durumuna ulaştığında kabul edecektir.

Sonlu bir otomat aşağıdakilerden oluşur:

Q: sonlu durumlar kümesi
∑: sonlu giriş sembolü kümesi
q0: başlangıç ​​durumu
F: son durum
d: Geçiş işlevi

Geçiş fonksiyonu şu şekilde tanımlanabilir:

 δ: Q x ∑ →Q 

FA iki şekilde karakterize edilir:

1. DFA (sonlu otomata)
2. NDFA (deterministik olmayan sonlu otomatlar)

DFA

DFA, Deterministik Sonlu Otomata anlamına gelir. Deterministik, hesaplamanın benzersizliğini ifade eder. DFA'da giriş karakteri yalnızca bir duruma gider. DFA, boş hareketi kabul etmez; bu, DFA'nın herhangi bir giriş karakteri olmadan durumu değiştiremeyeceği anlamına gelir.

DFA'da beş grup vardır {Q, ∑, q0, F, δ}

Örnek

Deterministik sonlu otomata örneğine bakın:

 Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q3}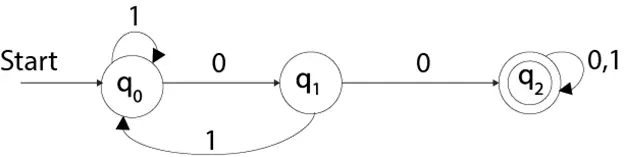 

NDFA

NDFA, Deterministik Olmayan Sonlu Otomatları ifade eder. Belirli bir giriş için herhangi bir sayıda durumu aktarmak için kullanılır. NDFA, NULL hareketini kabul eder; bu, sembolleri okumadan durumu değiştirebileceği anlamına gelir.

NDFA'nın da DFA ile aynı beş durumu vardır. Ancak NDFA'nın farklı geçiş işlevi vardır.

NDFA'nın geçiş işlevi şu şekilde tanımlanabilir:

Örnek

Deterministik olmayan sonlu otomatların bir örneğine bakın:

 Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q3}