Dinamik programlama, problemleri alt problemlere bölen ve sonucu tekrar hesaplamamıza gerek kalmaması için sonucu gelecekteki amaçlar için saklayan bir tekniktir. Alt problemler, optimal altyapı özelliği olarak bilinen genel çözümü optimize etmek için optimize edilir. Dinamik programlamanın temel kullanımı optimizasyon problemlerini çözmektir. Burada optimizasyon problemleri, bir problemin minimum veya maksimum çözümünü bulmaya çalıştığımız anlamına gelir. Dinamik programlama, eğer çözüm mevcutsa, bir problemin en uygun çözümünü bulmayı garanti eder.
Dinamik programlamanın tanımı, karmaşık bir problemi önce daha basit alt problemlerden oluşan bir koleksiyona bölerek, her bir alt problemi yalnızca bir kez çözerek ve ardından tekrarlayan hesaplamalardan kaçınmak için çözümlerini saklayarak çözme tekniği olduğunu söyler.
Bu yaklaşımı bir örnek üzerinden anlayalım.
Fibonacci serisinin bir örneğini düşünün. Aşağıdaki seri Fibonacci serisidir:
java sayacı
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ,…
Yukarıdaki serideki sayılar rastgele hesaplanmamıştır. Matematiksel olarak, aşağıdaki formülü kullanarak terimlerin her birini yazabiliriz:
F(n) = F(n-1) + F(n-2),
Temel değerler F(0) = 0 ve F(1) = 1'dir. Diğer sayıları hesaplamak için yukarıdaki ilişkiyi takip ederiz. Örneğin, F(2) toplamıdır f(0) Ve f(1), bu da 1'e eşittir.
F(20)'yi nasıl hesaplayabiliriz?
F(20) terimi Fibonacci serisinin n'inci formülü kullanılarak hesaplanacaktır. Aşağıdaki şekil F(20)'nin nasıl hesaplandığını göstermektedir.
veri yapıları java
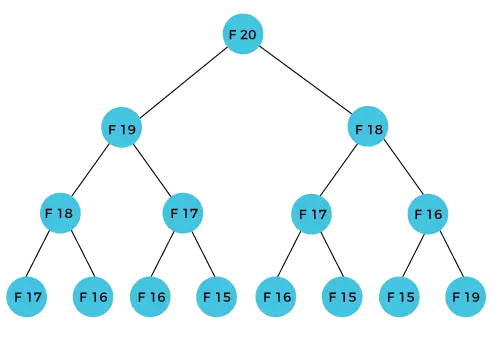
Yukarıdaki şekilde görüldüğü gibi F(20), F(19) ve F(18)'in toplamı olarak hesaplanmaktadır. Dinamik programlama yaklaşımında problemi benzer alt problemlere bölmeye çalışırız. Yukarıdaki durumda F(20)'nin benzer alt problemlere, yani F(19) ve F(18)'e dönüştürüldüğü durumda bu yaklaşımı izliyoruz. Dinamik programlamanın tanımını özetlersek, benzer alt problemin birden fazla hesaplanmaması gerektiğini söylüyor. Yine de yukarıdaki durumda alt problem iki kez hesaplanır. Yukarıdaki örnekte F(18) iki kez hesaplanır; benzer şekilde F(17) de iki kez hesaplanır. Ancak bu teknik benzer alt problemleri çözdüğü için oldukça kullanışlıdır ancak sonuçları saklarken dikkatli olmamız gerekir çünkü hesapladığımız sonucu bir kez saklama konusunda titiz değiliz, daha sonra kaynak israfına yol açabilir.
Yukarıdaki örnekte sağ alt ağaçta F(18) değerini hesaplarsak, bu durum kaynakların çok fazla kullanılmasına ve genel performansın düşmesine neden olur.
Yukarıdaki problemin çözümü hesaplanan sonuçları bir diziye kaydetmektir. Öncelikle F(16) ve F(17)'yi hesaplayıp değerlerini bir diziye kaydediyoruz. F(18), halihazırda bir diziye kayıtlı olan F(17) ve F(16) değerlerinin toplanmasıyla hesaplanır. F(18)'in hesaplanan değeri bir diziye kaydedilir. F(19)'un değeri, F(18) ve F(17)'nin toplamı kullanılarak hesaplanır ve değerleri zaten bir diziye kaydedilmiştir. F(19)'un hesaplanan değeri bir dizide saklanır. F(20) değeri, F(19) ve F(18) değerlerinin toplanmasıyla hesaplanabilir ve hem F(19) hem de F(18) değerleri bir dizide saklanır. F(20)'nin hesaplanan son değeri bir dizide saklanır.
Dinamik programlama yaklaşımı nasıl çalışır?
Dinamik programlamanın izlediği adımlar şunlardır:
- Karmaşık problemi daha basit alt problemlere ayırır.
- Bu alt problemlere en uygun çözümü bulur.
- Alt problemlerin sonuçlarını saklar (notlandırma). Alt problemlerin sonuçlarının saklanması işlemi ezberleme olarak bilinir.
- Aynı alt problemin birden fazla hesaplanması için bunları yeniden kullanır.
- Son olarak karmaşık problemin sonucunu hesaplayın.
Yukarıdaki beş adım dinamik programlamanın temel adımlarıdır. Dinamik programlama aşağıdaki gibi özelliklere sahip olduğunda uygulanabilir:
işletim sisteminin kullanım alanları
Üst üste binen alt problemlere ve optimal altyapılara sahip olan problemler. Burada optimal altyapı, optimizasyon problemlerinin çözümünün, tüm alt problemlerin optimal çözümünün basit bir şekilde birleştirilmesiyle elde edilebileceği anlamına gelir.
Dinamik programlama durumunda, ara sonuçları sakladığımızda uzay karmaşıklığı artacak, ancak zaman karmaşıklığı azalacaktır.
Dinamik programlama yaklaşımları
Dinamik programlamaya iki yaklaşım vardır:
- Yukarıdan aşağıya yaklaşım
- Aşağıdan yukarıya yaklaşım
Yukarıdan aşağıya yaklaşım
Yukarıdan aşağıya yaklaşım ezberleme tekniğini takip ederken aşağıdan yukarıya yaklaşım tablolaştırma yöntemini takip eder. Burada ezberleme, özyineleme ve önbelleğe almanın toplamına eşittir. Özyineleme, işlevin kendisini çağırmak anlamına gelirken önbelleğe alma, ara sonuçları depolamak anlamına gelir.
Avantajları
- Anlaşılması ve uygulanması oldukça kolaydır.
- Alt problemleri ancak gerektiğinde çözer.
- Hata ayıklamak kolaydır.
Dezavantajları
sınırlayıcıyı ayarla java
Çağrı yığınında daha fazla bellek kaplayan özyineleme tekniğini kullanır. Bazen özyineleme çok derin olduğunda yığın taşması durumu ortaya çıkar.
Genel performansı düşüren daha fazla bellek kaplar.
Bir örnek üzerinden dinamik programlamayı anlayalım.
int fib(int n) { if(n<0) error; if(n="=0)" return 0; 1; sum="fib(n-1)" + fib(n-2); } < pre> <p>In the above code, we have used the recursive approach to find out the Fibonacci series. When the value of 'n' increases, the function calls will also increase, and computations will also increase. In this case, the time complexity increases exponentially, and it becomes 2<sup>n</sup>.</p> <p>One solution to this problem is to use the dynamic programming approach. Rather than generating the recursive tree again and again, we can reuse the previously calculated value. If we use the dynamic programming approach, then the time complexity would be O(n).</p> <p>When we apply the dynamic programming approach in the implementation of the Fibonacci series, then the code would look like:</p> <pre> static int count = 0; int fib(int n) { if(memo[n]!= NULL) return memo[n]; count++; if(n<0) error; if(n="=0)" return 0; 1; sum="fib(n-1)" + fib(n-2); memo[n]="sum;" } < pre> <p>In the above code, we have used the memorization technique in which we store the results in an array to reuse the values. This is also known as a top-down approach in which we move from the top and break the problem into sub-problems.</p> <h3>Bottom-Up approach</h3> <p>The bottom-up approach is also one of the techniques which can be used to implement the dynamic programming. It uses the tabulation technique to implement the dynamic programming approach. It solves the same kind of problems but it removes the recursion. If we remove the recursion, there is no stack overflow issue and no overhead of the recursive functions. In this tabulation technique, we solve the problems and store the results in a matrix.</p> <p>There are two ways of applying dynamic programming:</p> <ul> <tr><td>Top-Down</td> </tr><tr><td>Bottom-Up</td> </tr></ul> <p>The bottom-up is the approach used to avoid the recursion, thus saving the memory space. The bottom-up is an algorithm that starts from the beginning, whereas the recursive algorithm starts from the end and works backward. In the bottom-up approach, we start from the base case to find the answer for the end. As we know, the base cases in the Fibonacci series are 0 and 1. Since the bottom approach starts from the base cases, so we will start from 0 and 1.</p> <p> <strong>Key points</strong> </p> <ul> <li>We solve all the smaller sub-problems that will be needed to solve the larger sub-problems then move to the larger problems using smaller sub-problems.</li> <li>We use for loop to iterate over the sub-problems.</li> <li>The bottom-up approach is also known as the tabulation or table filling method.</li> </ul> <p> <strong>Let's understand through an example.</strong> </p> <p>Suppose we have an array that has 0 and 1 values at a[0] and a[1] positions, respectively shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-2.webp" alt="Dynamic Programming"> <p>Since the bottom-up approach starts from the lower values, so the values at a[0] and a[1] are added to find the value of a[2] shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-3.webp" alt="Dynamic Programming"> <p>The value of a[3] will be calculated by adding a[1] and a[2], and it becomes 2 shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-4.webp" alt="Dynamic Programming"> <p>The value of a[4] will be calculated by adding a[2] and a[3], and it becomes 3 shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-5.webp" alt="Dynamic Programming"> <p>The value of a[5] will be calculated by adding the values of a[4] and a[3], and it becomes 5 shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-6.webp" alt="Dynamic Programming"> <p>The code for implementing the Fibonacci series using the bottom-up approach is given below:</p> <pre> int fib(int n) { int A[]; A[0] = 0, A[1] = 1; for( i=2; i<=n; i++) { a[i]="A[i-1]" + a[i-2] } return a[n]; < pre> <p>In the above code, base cases are 0 and 1 and then we have used for loop to find other values of Fibonacci series.</p> <p> <strong>Let's understand through the diagrammatic representation.</strong> </p> <p>Initially, the first two values, i.e., 0 and 1 can be represented as:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-7.webp" alt="Dynamic Programming"> <p>When i=2 then the values 0 and 1 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-8.webp" alt="Dynamic Programming"> <p>When i=3 then the values 1and 1 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-9.webp" alt="Dynamic Programming"> <p>When i=4 then the values 2 and 1 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-10.webp" alt="Dynamic Programming"> <p>When i=5, then the values 3 and 2 are added shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/79/dynamic-programming-11.webp" alt="Dynamic Programming"> <p>In the above case, we are starting from the bottom and reaching to the top.</p> <hr></=n;></pre></0)></pre></0)>