- DFA, deterministik sonlu otomatları ifade eder. Deterministik, hesaplamanın benzersizliğini ifade eder. Makine bir giriş dizesini her defasında bir sembol olarak okuyorsa, sonlu otomatlara deterministik sonlu otomatlar denir.
- DFA'da belirli girdiler için geçerli durumdan sonraki duruma yalnızca tek bir yol vardır.
- DFA boş hareketi kabul etmez, yani DFA herhangi bir giriş karakteri olmadan durumu değiştiremez.
- DFA birden fazla son durum içerebilir. Derleyicide Sözcüksel Analizde kullanılır.
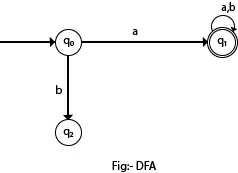
Aşağıdaki diyagramda a girişi için q0 durumundan q1'e giden tek bir yol olduğunu görebiliriz. Benzer şekilde, q0'dan b girişi için q2'ye giden tek bir yol vardır.
DFA'nın Resmi Tanımı
DFA, FA tanımında tanımladığımız gibi 5'li kümelerden oluşan bir koleksiyondur.
c dilinde matris
Q: finite set of states ∑: finite set of the input symbol q0: initial state F: final state δ: Transition function
Geçiş fonksiyonu şu şekilde tanımlanabilir:
δ: Q x ∑→Q
DFA'nın Grafiksel Gösterimi
Bir DFA, durum diyagramı adı verilen digraflarla temsil edilebilir. Hangisinde:
- Durum köşelerle temsil edilir.
- Giriş karakteriyle etiketlenen yay, geçişleri gösterir.
- Başlangıç durumu bir okla işaretlenmiştir.
- Son durum çift daire ile gösterilir.
Örnek 1:
Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q2} Çözüm:
Geçiş Şeması:

Geçiş Tablosu:
| Mevcut durum | Giriş 0 için sonraki durum | Giriş 1'in Sonraki Durumu |
|---|---|---|
| →q0 | q0 | q1 |
| q1 | q2 | q1 |
| *q2 | q2 | q2 |
Örnek 2:
∑ = {0, 1} olan DFA, 0 ile başlayanların tümünü kabul eder.
Çözüm:

Açıklama:
dize karşılaştırma c#
- Yukarıdaki şemada, q0 durumunda DFA'ya giriş olarak 0 verildiğinde DFA'nın durumunu q1 olarak değiştirdiğini ve 0 girişi başlatıldığında her zaman son durum q1'e gittiğini görebiliriz. 00, 01, 000, 001...'i kabul edebilir... .vesaire. 1 ile başlayan herhangi bir dizeyi kabul edemez çünkü 1 ile başlayan bir dizede asla son duruma gitmez.
Örnek 3:
∑ = {0, 1} olan DFA, 0 ile biten tüm işlemleri kabul eder.
Çözüm:

Açıklama:
Yukarıdaki diyagramda, q0 durumunda DFA'ya giriş olarak 0 verildiğinde DFA'nın durumunu q1 olarak değiştirdiğini görebiliriz. 00, 10, 110, 100... vb. gibi 0 ile biten herhangi bir diziyi kabul edebilir. Sonu 1 ile biten herhangi bir diziyi kabul edemez çünkü 1 girişte asla q1 son durumuna gitmez, yani 1 ile biten dize kabul edilmez veya reddedilir.
