- Bitsel XOR operatörü aynı zamanda şu şekilde de bilinir: Özel veya
- Kullanılarak gösterilir '^'
- Adından da anlaşılacağı gibi, üzerinde çalışır bit seviyesi işlenenlerden.
- Bitwise XOR operatörü, Bitwise operatörleri kategorisine girmiştir.
- Bit düzeyinde özel OR operatöründe (XOR), iki işlenen gereklidir ve bu iki işlenen, XOR sembolüyle, yani '^' ile ayrılır.
- XOR operatörünü iki işlenene uyguladıktan sonra ortaya çıkan çıktıyı veya sonucu belirlemek için XOR operatörünün Mantıksal doğruluk tablosunu takip etmemiz gerekir.
- XOR Doğruluk Tablosu, XOR operatörünün uygun mantığı kullanılarak oluşturulan matematiksel tablodur.
- XOR operatörünün arkasında kullanılan mantık; ikisine XOR işlemi uygulandığında farklı iki işlenenin bitleri, o zaman sonuç her zaman üretilecektir '1', ve eğer XOR işlemi ikisine uygulanırsa Aynı iki işlenenin bitleri daha sonra sonuç çıktı üretir '0'.
Özel OR (XOR) operatörünün Doğruluk Tablosu
İki işlenen olsun; Birincisi A ve ikincisi B ise bu iki işlenenin oluşturduğu toplam giriş kombinasyonları 4 olacaktır. Aşağıdaki XOR doğruluk tablosunu kullanarak karşılık gelen çıkışı belirleyeceğiz. Sonuç burada C'de yakalanacak C = A ^ B.
Bu doğruluk tablosunda girdiyi bit şeklinde yani 0 ve 1 olarak alıyoruz ve çıktı da bit biçiminde yani 0 ve 1 şeklinde üretilecek.
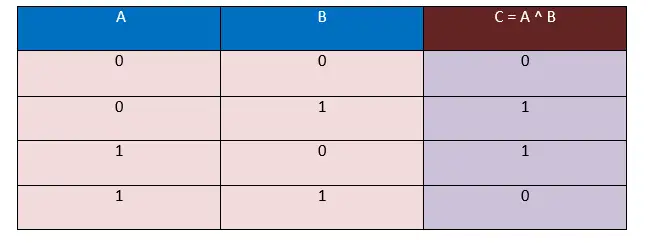
Burada, yukarıdaki XOR Doğruluk tablosunda, A ve B işlenenlerinin değerleri farklı olduğunda, yani ( 0, 1 ), ( 1, 0 ), ortaya çıkan sonucun her zaman 1 olacağını gözlemliyoruz. A ve B işlenenlerinin değerleri aynıysa, yani ( 0, 0 ), ( 1, 1 ), ortaya çıkan sonuç her zaman 0 olacaktır.
Benzer şekilde bu şekilde doğruluk tablosunu da çizebiliriz. Boolean değerler -
İki işlenen olsun; birincisi A ve ikincisi B . Bu iki işlenenin oluşturduğu toplam giriş kombinasyonları 4 olacaktır. Aşağıdaki XOR doğruluk tablosunu kullanarak karşılık gelen çıkışı belirleyeceğiz. Sonuç C'de yakalanacaktır, burada C = A ^ B.
Bu doğruluk tablosunda Doğruluk değerleri biçiminde girdi alıyoruz, yani Doğru (T) ve Yanlış (F). Çıktı aynı zamanda Gerçek değerler, yani T ve F biçiminde de üretilecektir.

Burada, yukarıdaki XOR Doğruluk tablosunda, A ve B işlenenlerinin değerleri farklı olduğunda, yani ( F, T ), ( T, F ), sonucun her zaman T olacağını görüyoruz. A ve B işlenenlerinin değerleri aynıysa, yani ( F, F ), ( T, T ), sonuç her zaman F olacaktır.
Yukarıdaki tablolardan şunu görüyoruz. T (Doğru) bir ile, F (Yanlış) ise 0 ile gösterilir.
Herhangi bir sorunu çözme adımları -
- Problemde verilen işlenenler her zaman ondalık değerde olacaktır.
- Öncelikle işlenenlerin değerlerini şuna dönüştürmemiz gerekir: ikili
- İşlenenlerin değerlerini ikili sayılara dönüştürdükten sonra, her iki işleneni üst üste koyun.
- Bunlara özel VEYA (XOR) işlemi uygulamadan önce lütfen kontrol edin. Basamak sayısı onların içinde.
- Rakamların sayısı eşleşmiyorsa, küçük işlenenin sol ucundaki fazladan 0'lar rakam sayılarını dengeler.
- Son olarak, yukarıdaki doğruluk tablosunun yardımıyla, XOR işlemini uygulamak için her seferinde bir bit alarak işlenenlere tek tek XOR işlemini uygulayın.
- Sonunda sonuç çıktı biçiminde üretilir.
- Çıktı ikili formda olacaktır, şimdi ikili formu ondalık forma dönüştürün ve sonuç değerini not edin.
C++'da Bitsel Özel OR (XOR) işleminin yürütülmesi
Örneklerin yardımıyla XOR işleminin C++'da yürütülmesini daha ayrıntılı olarak anlayalım -
Örnek 1: Tamsayı değerlerinin özel VEYA değerini bulun; 10 ve 14. Ayrıca bunu açıklayın ve C++ yürütme kodunu yazın.
Çözüm: Yukarıdaki soruda verilen karşılık gelen iki işleneni, yani 10 ve 14'ü depolamak için 'a' ve 'b' gibi iki değişkeni ele alalım.
Burada a = 10 ve b = 14.
Verilen iki işlenenin özel VEYA değerini bulmak için aşağıdaki adımları izleyeceğiz.
- 10 ve 14'ün ondalık formda olduğunu ve bitsel XOR işlemi uygulamak için onu ikili forma dönüştürmek gerektiğini biliyoruz.
- 'a' ikili formu, yani 10 '1010' ve 'b'nin ikili biçimi, yani 14 '1110'.
- Burada a'da bulunan ikili rakamların sayısının dört, b'de bulunan ikili rakamların sayısının da 4 olduğunu görüyoruz; dolayısıyla her iki değişkende de bulunan ikili basamakların sayısı aynıdır ve zaten dengelidir, dengelemek için daha fazla 0 eklememize gerek yoktur.
- Şimdi, 'b'de bulunan ikili rakamları 'a'da bulunan ikili rakamlara indiriyoruz.
- Son olarak ilgili bitler üzerinde XOR işlemini tek tek uygulayarak çıktıyı not edin.
- Sonunda oluşturulan çıktı, yukarıdaki soruda ondalık formda verildiği gibi ikili formda olacaktır, bu nedenle sonucu ondalık forma dönüştürmemiz gerekir.
Açıklama:
a = 10 (Ondalık Biçimde)
b = 14 (Ondalık Formda)
Şimdi bir XOR b için a ve b'yi ikili biçimde dönüştürmemiz gerekiyor -
a = 1010 (İkili biçimde)
b = 1110 (İkili biçimde)
Şimdi a ve b'ye XOR işlemini uyguluyoruz -
bir = 1010
b = 1110
---------------
a ^ b = 0100 (İkili formda)
a ^ b'nin sonucu ikili formda olan 0100'dür.
Şimdi sonucu 4 olan ondalık biçime dönüştürüyoruz.
10^14 = 4
NOT: Yukarıdaki XOR doğruluk tablosu kullanılarak karşılık gelen bitlerin çıktısı oluşturulur.
Şimdi C++ dilinde 10 ve 14'e bitsel XOR işlemini uygulayacağız ve sonucu yani 4'ü elde edeceğiz.
Yukarıdaki örnek için C++ kodu:
//************************ C++ Code ****************************** #include using namespace std; int main () { int a, b, c ; // Initializing integer variables to store data values cout <' << endl ; cout <> a ; // taking a as input from user cout <> b ; // taking b as input from user c = a ^ b ; // storing XOR result of a and b in c cout << 'Applying XOR operation on a and b: '<< endl ; cout << 'a ^ b = ' << c << endl ; // Printing the output } </'> Çıktı

Örnek 2: Tamsayı değerlerinin özel VEYA değerini bulun; 3 ve 15. Ayrıca bunu açıklayın ve C++ yürütme kodunu yazın.
Çözüm: Yukarıdaki soruda verilen karşılık gelen iki işleneni, yani 3 ve 15'i depolamak için 'a' ve 'b' gibi iki değişkeni ele alalım.
postgres'te seri
Burada a = 3 ve b = 15.
Verilen iki işlenenin özel VEYA değerini bulmak için aşağıdaki adımları izleyeceğiz.
- 3 ve 15'in ondalık formda olduğunu ve bitsel XOR işlemi uygulamak için onu ikili forma dönüştürmek gerektiğini biliyoruz.
- 'a' ikili formu, yani 3 'onbir' ve 'b'nin ikili biçimi, yani 15 '1111'.
- Burada a'da bulunan ikili rakamların sayısının iki, b'de bulunan ikili rakamların sayısının dört olduğunu gözlemleyeceğiz; dolayısıyla her iki değişkende bulunan ikili basamakların sayısı aynı değildir. Bu nedenle, dengesiz olduğunda, alt ikili sayının, yani 'a'nın sol tarafına daha fazla sayıda 0 eklememiz gerekir. onbir' , dengelemek için.
- Dengelemeden sonra a'nın değeri '0011' ve b '1111'.
- Şimdi 'b'de bulunan ikili rakamları 'a'da bulunan ikili rakamlara indiriyoruz.
- Son olarak ilgili bitler üzerinde XOR işlemini tek tek uygulayarak çıktıyı not edin.
- Sonunda oluşturulan çıktı, yukarıdaki soruda ondalık formda verildiği gibi ikili formda olacaktır, bu nedenle sonucu ondalık forma dönüştürmemiz gerekir.
Açıklama:
a = 3 (Ondalık Biçimde)
b = 15 (Ondalık Biçimde)
Şimdi bir XOR b için a ve b'yi ikili biçimde dönüştürmemiz gerekiyor -
a = 0011 (İkili biçimde)
b = 1111 (İkili biçimde)
Şimdi a ve b'ye XOR işlemini uyguluyoruz -
bir = 0011
b = 1111
---------------
a ^ b = 1100 (İkili formda)
a ^ b'nin sonucu ikili formda olan 1100'dür.
Şimdi sonucu 12 olan ondalık biçime dönüştürüyoruz.
3^15 = 12
NOT: Yukarıdaki XOR doğruluk tablosu kullanılarak karşılık gelen bitlerin çıktısı oluşturulur.
Şimdi C++ dilinde 3 ve 15'e bitsel XOR işlemini uygulayacağız ve sonucu yani 12'yi elde edeceğiz.
Yukarıdaki örnek için C++ kodu:
//************************ C++ Code ****************************** #include using namespace std; int main () { int a, b, c ; // Initializing integer variables to store data values cout <' << endl ; cout <> a ; // taking a as input from user cout <> b ; // taking b as input from user c = a ^ b ; // storing XOR result of a and b in c cout << 'Applying XOR operation on a and b: '<< endl ; cout << 'a ^ b = ' << c << endl ; // Printing the output } </'> Çıktı

