Matematikte her yerde çizginin bir uygulaması vardır. Her yerde, yani geometride, cebirde ve diğerlerinde uygulanır. Eğim çizginin yönünü tanımlar.
Bu yazıda tanımsız eğim ve sıfır eğim olmak üzere iki tür eğimi tartışacağız. Eğim türlerini anlamadan önce eğimin kısa tanımına bakalım.
javascript'e tıkla
Eğim nedir?
Eğim şunu tanımlar: diklik hattın. 'Diklik' kelimesi çizginin ne kadar eğimli olduğu anlamına gelir. Başka bir deyişle eğim, koordinat düzlemindeki bir doğrunun yönünü gösterir. Bu nedenle bir çizginin gradyanı olarak da bilinir. Rampa, merdiven vb. eğimin gerçek hayattaki örneklerinden bazılarıdır.
Matematikte eğim, iki nokta arasındaki 'yükselişin' 'uzunluk'a oranıdır. 'Yükseliş' çizgideki dikey değişimi, 'Koş' ise çizgideki yatay değişimi ifade eder.
İki nokta arasındaki çizginin eğimi (x1, Ve1) ve (x2, Ve2) noktaların koordinatları arasındaki fark bulunarak belirlenebilir. Bir doğrunun eğimi genellikle 'm' harfiyle gösterilir.
m = Δx/Δy = (y2- Ve1)/(X2- X1)veya m = yükselme/koşma
Tanımsız eğim
Tanımsız eğim dikey çizginin eğimidir. Bu, eğer doğru dikeyse eğimin tanımsız olduğu anlamına gelir. Tanımsız eğimdeki doğru y eksenine paraleldir ve ?x'in değeri 0'dır. Tanımsız eğimin x koordinatı, y koordinatı ne olursa olsun asla değişmez. Tanımsız bir eğimde Δy değeri sıfır olmayan bir tamsayı iken Δx değeri 0'dır. Tanımsız eğim sıfır eğimin tersidir. Yükseliş ve mesafe açısından, tanımsız eğimdeki artış ya pozitif ya da negatiftir ve tanımsız eğimdeki mesafe sıfırdır.
m = Δy/Δx = pozitif veya negatif Δy/0M'nin tanımsız değeri tanımsız eğimi ve dikey çizgiyi temsil eder.
Aşağıdaki grafikte tanımsız bir eğimin gösterimini görebilirsiniz. Aşağıdaki grafikteki çizgi tanımsız eğimi ifade eden y eksenine paraleldir.
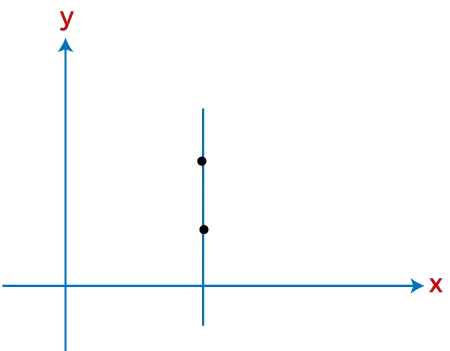
Şekil: Tanımsız eğimin temsili
Yukarıdaki görselde tanımsız eğimi gösteren dikey bir çizgi bulunmaktadır.
Sıfır eğim
Sıfır eğimde doğru x eksenine paraleldir ve y koordinatı hiçbir zaman değişmez. Yatay çizginin eğimidir. Yükseliş ve ilerleme açısından sıfır eğimdeki artış 0, sıfır eğimdeki ilerleme ise pozitiftir.
m = Δy/Δx = 0/pozitif ΔxM değeri sıfıra eşitse doğru yataydır ve sabit bir eğime sahiptir.
Aşağıdaki grafikte sıfır eğimin gösterimini görebilirsiniz. Aşağıdaki grafikteki çizgi sıfır eğimi ifade eden x eksenine paraleldir ve sıfır eğimdeki y, x ne olursa olsun aynı kalır.

Şekil: Sıfır eğimin temsili
Yukarıdaki görselde sıfır eğimi gösteren yatay bir çizgi bulunmaktadır.
Şimdi tanımsız eğim ile sıfır eğim arasındaki farkı görelim.
Tanımsız eğim ile Sıfır eğim arasındaki fark
Tanımsız eğim Sıfır eğimin tersidir. Tanımsız eğim ile sıfır eğim arasındaki fark aşağıdaki şekilde tablolanmıştır:
| Evet Hayır. | Tanımsız eğim | Sıfır eğim |
|---|---|---|
| 1. | X değişkeni tarafından belirlenir. | Y değişkeni tarafından belirlenir. |
| 2. | Dikey çizginin eğimidir. | Yatay çizginin eğimidir. |
| 3. | Tanımsız eğimin somut bir değeri olmadığı için var olmayan bir değeri vardır. | Sıfır eğim belirli bir değerdir, yani Sıfır. |
| 4. | Tanımsız eğimin paydası sıfırdır. | Sıfır eğimin payı sıfırdır. |
| 5. | Tanımsız bir eğimde Y değişir ancak X değişmez. | Tanımsız bir eğimde X değişir ancak Y değişmez. |
Makaleyle ilgili hepsi bu. Sizlere yeterli bilgiyi daha kolay bir şekilde vermeye çalıştık. Umarım işinize yarar ve tanımsız eğim, sıfır eğim ve bunların karşılaştırılması hakkında bilgi verir.
