• Aşağı açılan otomatlar, normal bir dilbilgisi için DFA'yı tasarladığımız şekilde bir CFG'yi uygulamanın bir yoludur. Bir DFA sınırlı miktarda bilgiyi hatırlayabilir, ancak bir PDA sonsuz miktarda bilgiyi hatırlayabilir.
• Aşağı açılan otomatlar basitçe 'harici yığın belleği' ile güçlendirilmiş bir NFA'dır. Yığın eklenmesi, Aşağı Açılan otomatlara son giren ilk çıkar bellek yönetimi yeteneği sağlamak için kullanılır. Aşağı açılan otomatlar yığında sınırsız miktarda bilgi depolayabilir. Yığındaki sınırlı miktarda bilgiye erişebilir. Bir PDA, bir öğeyi yığının tepesine itebilir ve bir öğeyi yığının tepesinden çıkarabilir. Yığına bir öğe okumak için üstteki öğelerin çıkarılması ve kaybolması gerekir.
• PDA, FA'dan daha güçlüdür. FA tarafından kabul edilebilen herhangi bir dil, PDA tarafından da kabul edilebilir. PDA aynı zamanda FA tarafından bile kabul edilemeyecek bir dil sınıfını da kabul etmektedir. Bu nedenle PDA, FA'dan çok daha üstündür.

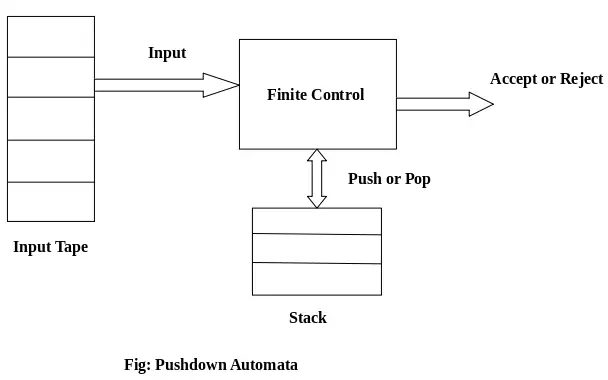
PDA Bileşenleri:

Giriş bandı: Giriş bandı birçok hücreye veya sembole bölünmüştür. Giriş başlığı salt okunurdur ve her defasında yalnızca bir sembol olmak üzere soldan sağa doğru hareket edebilir.

Sonlu kontrol: Sonlu kontrol, okunacak geçerli sembolü gösteren bazı işaretçilere sahiptir.

Yığın: Stack, eşyaları sadece bir ucundan itip çıkarabildiğimiz bir yapıdır. Sonsuz bir boyutu var. PDA'da yığın, öğeleri geçici olarak depolamak için kullanılır.

PDA'nın resmi tanımı:

PDA 7 bileşenin birleşimi olarak tanımlanabilir:

Q: sonlu durumlar kümesi

∑: giriş seti

C: yığından itilip çıkarılabilen bir yığın sembolü

q0: başlangıç ​​durumu

erkek arkadaşlar için algoritma

İLE: Γ'da olan bir başlangıç ​​sembolü.

F: bir dizi son durum

D: Mevcut durumdan sonraki duruma geçmek için kullanılan haritalama işlevi.

Anlık Açıklama (ID)

Kimlik, bir PDA'nın bir giriş dizesini nasıl hesapladığını ve bu dizenin kabul veya reddedilmesine nasıl karar verdiğini gösteren resmi olmayan bir gösterimdir.

Anlık bir açıklama üçlüdür (q, w, α):

Q mevcut durumu anlatır.

İçinde kalan girişi açıklar.

myflixr

A sol üstte yığın içeriğini açıklar.

Turnike Notasyonu:

⊢ işareti turnike gösterimini açıklar ve bir hareketi temsil eder.

⊢* işareti bir dizi hamleyi tanımlar.

Örneğin,

(p, b, T) ⊢ (q, w, α)

Yukarıdaki örnekte, p durumundan q durumuna geçiş yapılırken 'b' giriş sembolü tüketilir ve 'T' yığınının tepesi yeni bir α dizisi ile temsil edilir.

Örnek 1:

Bir dili kabul etmek için bir PDA tasarlayın^NB²ⁿ.

Çözüm: Bu dilde n adet a'nın ardından 2n adet b gelmelidir. Dolayısıyla çok basit bir mantık uygulayacağız, yani tek bir 'a' okursak yığına iki a'yı iteceğiz. 'b' okur okumaz, her bir 'b' için yığından yalnızca bir 'a' atılmalıdır.

json örneğinde json

Kimlik aşağıdaki gibi oluşturulabilir:

 δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa) 

Şimdi b'yi okuduğumuzda durumu q0'dan q1'e değiştireceğiz ve karşılık gelen 'a'yı açmaya başlayacağız. Buradan,

 δ(q0, b, a) = (q1, ε) 

Dolayısıyla bu 'b' harfini patlatma işlemi, tüm semboller okunmadığı sürece tekrarlanacaktır. Patlama eyleminin yalnızca q1 durumunda gerçekleştiğini unutmayın.

 δ(q1, b, a) = (q1, ε) 

Tüm b'leri okuduktan sonra, karşılık gelen tüm a'ların atılması gerekir. Dolayısıyla ε'yu giriş sembolü olarak okuduğumuzda yığında hiçbir şey olmamalıdır. Dolayısıyla hareket şu şekilde olacaktır:

 δ(q1, ε, Z) = (q2, ε) 

Nerede

turbo c++ indir

PDA = ({q0, q1, q2}, {a, b}, {a, Z}, δ, q0, Z, {q2})

ID'yi şu şekilde özetleyebiliriz:

 δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa) δ(q0, b, a) = (q1, ε) δ(q1, b, a) = (q1, ε) δ(q1, ε, Z) = (q2, ε) 

Şimdi bu PDA'yı 'aaabbbbbb' girdi dizisi için simüle edeceğiz.

 δ(q0, aaabbbbbb, Z) ⊢ δ(q0, aabbbbbb, aaZ) ⊢ δ(q0, abbbbbb, aaaaZ) ⊢ δ(q0, bbbbbb, aaaaaaZ) ⊢ δ(q1, bbbbb, aaaaaZ) ⊢ δ(q1, bbbb, aaaaZ) ⊢ δ(q1, bbb, aaaZ) ⊢ δ(q1, bb, aaZ) ⊢ δ(q1, b, aZ) ⊢ δ(q1, ε, Z) ⊢ δ(q2, ε) ACCEPT 

Örnek 2:

Bir dili kabul edecek bir PDA tasarlayın 0^N1^M0^N.

Çözüm: Bu PDA'da, n sayıda 0'ın ardından herhangi bir sayıda 1 ve ardından n sayıda 0 gelir. Dolayısıyla böyle bir PDA'nın tasarımının mantığı şu şekilde olacaktır:

İlk 0'larla karşılaştığınızda tüm 0'ları yığına itin. O zaman 1'i okursak hiçbir şey yapmayın. Daha sonra 0'ı okuyun ve her 0 okunduğunda yığından bir 0 çıkarın.

Örneğin:

Bu senaryo ID formunda şu şekilde yazılabilir:

 δ(q0, 0, Z) = δ(q0, 0Z) δ(q0, 0, 0) = δ(q0, 00) δ(q0, 1, 0) = δ(q1, 0) δ(q0, 1, 0) = δ(q1, 0) δ(q1, 0, 0) = δ(q1, ε) δ(q0, ε, Z) = δ(q2, Z) (ACCEPT state) 

Şimdi bu PDA'yı '0011100' giriş dizisi için simüle edeceğiz.

 δ(q0, 0011100, Z) ⊢ δ(q0, 011100, 0Z) ⊢ δ(q0, 11100, 00Z) ⊢ δ(q0, 1100, 00Z) ⊢ δ(q1, 100, 00Z) ⊢ δ(q1, 00, 00Z) ⊢ δ(q1, 0, 0Z) ⊢ δ(q1, ε, Z) ⊢ δ(q2, Z) ACCEPT