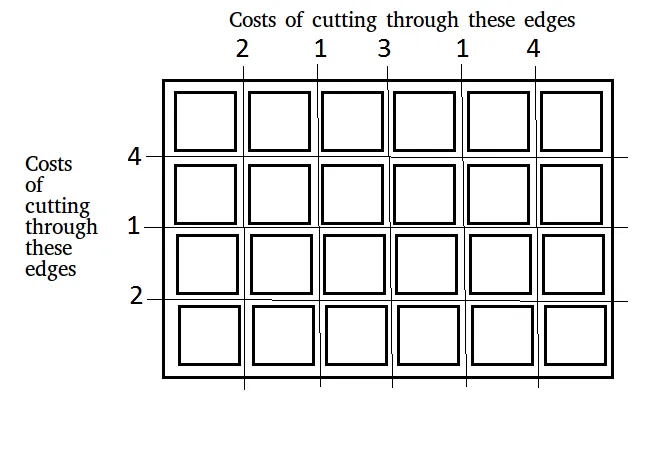
Bir boyut tablosu verildiğinde n × m bunun n × m karelere kesilmesi gerekiyor. Yatay veya dikey kenar boyunca kesim yapmanın maliyeti iki dizide sağlanır:
- X[] : Dikey kenarlar boyunca maliyetlerin azaltılması (uzunluk açısından).
- Ve[] : Yatay kenarlar boyunca maliyetlerin azaltılması (genişlik açısından).
Tahtayı en iyi şekilde karelere ayırmak için gereken minimum toplam maliyeti bulun.
Örnekler:
Giriş: x[] = [2 1 3 1 4] y[] = [4 1 2] n = 4 m = 6
Çıkış: 42
Açıklama:
Başlangıçta hayır. yatay bölümlerin sayısı = 1 & no. dikey bölümlerin sayısı = 1.
Kareye kesmenin en uygun yolu:
4'ü seçin (x'ten) -> dikey kesim Maliyet = 4 × yatay segmentler = 4
Şimdi yatay bölümler = 1 dikey bölüm = 2.
4'ü seçin (y'den) -> yatay kesim Maliyet = 4 × dikey segmentler = 8
Şimdi yatay bölümler = 2 dikey bölüm = 2.
3'ü seçin (x'ten) -> dikey kesim Maliyet = 3 × yatay segmentler = 6
Şimdi yatay bölümler = 2 dikey bölüm = 3.
2'yi seçin (x'ten) -> dikey kesim Maliyet = 2 × yatay segmentler = 4
Şimdi yatay bölümler = 2 dikey bölüm = 4.
2'yi seçin (y'den) -> yatay kesim Maliyet = 2 × dikey segmentler = 8
Şimdi yatay bölümler = 3 dikey bölüm = 4.
1'i seçin (x'ten) -> dikey kesim Maliyet = 1 × yatay segmentler = 3
Şimdi yatay bölümler = 3 dikey bölüm = 5.
1'i seçin (x'ten) -> dikey kesim Maliyet = 1 × yatay segmentler = 3
Şimdi yatay bölümler = 3 dikey bölüm = 6.
1'i seçin (y'den) -> yatay kesim Maliyet = 1 × dikey segmentler = 6
Şimdi yatay bölümler = 4 dikey bölüm = 6.
Yani toplam maliyet = 4 + 8 + 6 + 4 + 8 + 3 + 3 + 6 = 42.Giriş: x[] = [1 1 1] y[] = [1 1 1] n = 4 m = 4
Çıkış: 15
Açıklama:
Başlangıçta hayır. yatay bölümlerin sayısı = 1 & no. dikey bölümlerin sayısı = 1.
Kareye kesmenin en uygun yolu:
1'i seçin (y'den) -> yatay kesim Maliyet = 1 × dikey bölümler = 1
Şimdi yatay bölümler = 2 dikey bölüm = 1.
1'i seçin (y'den) -> yatay kesim Maliyet = 1 × dikey bölümler = 1
Şimdi yatay bölümler = 3 dikey bölüm = 1.
1'i seçin (y'den) -> yatay kesim Maliyet = 1 × dikey bölümler = 1
Şimdi yatay bölümler = 4 dikey bölüm = 1.
1'i seçin (x'ten) -> dikey kesim Maliyet = 1 × yatay segmentler = 4
Şimdi yatay bölümler = 4 dikey bölüm = 2.
1'i seçin (x'ten) -> dikey kesim Maliyet = 1 × yatay segmentler = 4
Şimdi yatay bölümler = 4 dikey bölüm = 3.
1'i seçin (x'ten) -> dikey kesim Maliyet = 1 × yatay segmentler = 4
Şimdi yatay bölümler = 4 dikey bölüm = 4
Yani toplam maliyet = 1 + 1 + 1 + 4 + 4 + 4 = 15.
İçerik Tablosu
- [Naif Yaklaşım] Tüm Permütasyonları Deneyin - O((n+m)!×(n+m)) Zaman ve O(n+m) Uzay
- [Beklenen Yaklaşım] Açgözlü Tekniği Kullanma - O( n (log n)+m (log m)) Zaman ve O(1) Uzay
[Naif Yaklaşım] Tüm Permütasyonları Deneyin - O((n+m)!×(n+m)) Zaman ve O(n+m) Uzay
Buradaki fikir, verilen kesintilerin tüm olası permütasyonlarını oluşturmak ve ardından her permütasyon için maliyeti hesaplamaktır. Son olarak aralarında minimum maliyeti döndürün.
Not: Bu yaklaşım daha büyük girdiler için uygun değildir çünkü permütasyon sayısı (m+n-2)! olarak faktöriyel olarak artar.
Her permütasyon için maliyeti O(m+n) zaman cinsinden hesaplamalıyız. Dolayısıyla toplam zaman karmaşıklığı O((m+n−2)!×(m+n)) olur.
[Beklenen Yaklaşım] Açgözlü Tekniği Kullanma - O( n (log n)+m (log m)) Zaman ve O(1) Uzay
Buradaki fikir, en pahalı kesimleri önce bir açgözlü yaklaşım . Gözlem, her adımda en yüksek maliyet kesintisinin seçilmesinin birden fazla parçayı aynı anda etkileyerek gelecekteki maliyetleri azalttığı yönündedir. Dikey (x) ve yatay (y) kesinti maliyetlerini azalan sırada sıralıyoruz ve ardından maliyet tasarrufunu en üst düzeye çıkarmak için yinelemeli olarak daha büyük olanı seçiyoruz. Kalan kesimler, tüm bölümlerin en iyi şekilde bölünmesini sağlamak için ayrı ayrı işlenir.
Kesim yaptığımızda ne olur?
- Yatay kesim → genişlik boyunca kesiyorsunuz, böylece yatay şeritlerin sayısı artıyor (hCount++). Ancak yatay kesimin tüm dikey bölümlerden geçmesi gerektiğinden maliyet vCount (dikey şerit sayısı) ile çarpılır.
- Dikey kesim → yükseklik boyunca kesiyorsunuz, böylece dikey şeritlerin sayısı artıyor (vCount++). Ancak dikey kesimin tüm yatay bölümlerden geçmesi gerektiğinden maliyet hCount (yatay şerit sayısı) ile çarpılır.
Sorunu çözmek için adımlar:
- Hem x hem de y dizilerini azalan düzende sıralayın.
- En büyük değerden başlayıp daha küçük değerlere doğru ilerleyerek biri x için, diğeri y için iki işaretçi kullanın.
- Her bir kesimin kaç segmenti etkilediğini izlemek ve bunları buna göre güncellemek için hCount ve vCount'u koruyun.
- Hem x hem de y işlenmemiş kesintilere sahipken, genel giderleri en aza indirmek için her zaman daha büyük maliyeti seçerek yineleyin.
- Eğer x'te kalan kesikler varsa bunları hCount çarpanıyla işleyin; kalan y kesimlerini de benzer şekilde vCount ile işleyin.
- Şu formülü kullanarak her adımda toplam maliyeti toplayın: maliyeti azaltın * minimum maliyet sağlayan etkilenen parça sayısı.
#include
import java.util.Arrays; class GfG { static int minCost(int n int m int[] x int[] y) { // Sort the cutting costs in ascending order Arrays.sort(x); Arrays.sort(y); int hCount = 1 vCount = 1; int i = x.length - 1 j = y.length - 1; int totalCost = 0; while (i >= 0 && j >= 0) { // Choose the larger cost cut to // minimize future costs if (x[i] >= y[j]) { totalCost += x[i] * hCount; vCount++; i--; } else { totalCost += y[j] * vCount; hCount++; j--; } } // Process remaining vertical cuts while (i >= 0) { totalCost += x[i] * hCount; vCount++; i--; } // Process remaining horizontal cuts while (j >= 0) { totalCost += y[j] * vCount; hCount++; j--; } return totalCost; } public static void main(String[] args) { int n = 4m = 6; int[] x = {2 1 3 1 4}; int[] y = {4 1 2}; System.out.println(minCost(n m x y)); } }
def minCost(nm x y): # Sort the cutting costs in ascending order x.sort() y.sort() hCount vCount = 1 1 i j = len(x) - 1 len(y) - 1 totalCost = 0 while i >= 0 and j >= 0: # Choose the larger cost cut to # minimize future costs if x[i] >= y[j]: totalCost += x[i] * hCount vCount += 1 i -= 1 else: totalCost += y[j] * vCount hCount += 1 j -= 1 # Process remaining vertical cuts while i >= 0: totalCost += x[i] * hCount vCount += 1 i -= 1 # Process remaining horizontal cuts while j >= 0: totalCost += y[j] * vCount hCount += 1 j -= 1 return totalCost if __name__ == '__main__': nm = 4 6 x = [2 1 3 1 4] y = [4 1 2] print(minCost(nmx y))
using System; class GfG { public static int minCost(int n int m int[] x int[] y) { // Sort the cutting costs in ascending order Array.Sort(x); Array.Sort(y); int hCount = 1 vCount = 1; int i = x.Length - 1 j = y.Length - 1; int totalCost = 0; // Process the cuts in greedy manner while (i >= 0 && j >= 0) { // Choose the larger cost cut to // minimize future costs if (x[i] >= y[j]) { totalCost += x[i] * hCount; vCount++; i--; } else { totalCost += y[j] * vCount; hCount++; j--; } } // Process remaining vertical cuts while (i >= 0) { totalCost += x[i] * hCount; vCount++; i--; } // Process remaining horizontal cuts while (j >= 0) { totalCost += y[j] * vCount; hCount++; j--; } return totalCost; } public static void Main() { int n=4m=6; int[] x = {2 1 3 1 4}; int[] y = {4 1 2}; Console.WriteLine(minCost(nm x y)); } }
function minCost( nm x y) { // Sort the cutting costs in ascending order x.sort((a b) => a - b); y.sort((a b) => a - b); let hCount = 1 vCount = 1; let i = x.length - 1 j = y.length - 1; let totalCost = 0; while (i >= 0 && j >= 0) { // Choose the larger cost cut to // minimize future costs if (x[i] >= y[j]) { totalCost += x[i] * hCount; vCount++; i--; } else { totalCost += y[j] * vCount; hCount++; j--; } } // Process remaining vertical cuts while (i >= 0) { totalCost += x[i] * hCount; vCount++; i--; } // Process remaining horizontal cuts while (j >= 0) { totalCost += y[j] * vCount; hCount++; j--; } return totalCost; } // Driver Code let n = 4m = 6; let x = [2 1 3 1 4]; let y = [4 1 2]; console.log(minCost(nm x y));
Çıkış
42