Silme işlevi, belirtilen düğümü ikili arama ağacından silmek için kullanılır. Ancak ikili arama ağacındaki bir düğümü, ikili arama ağacının özelliğini ihlal etmeyecek şekilde silmeliyiz. Bir düğümün ikili arama ağacından silinmesinin üç durumu vardır.
Silinecek düğüm bir yaprak düğümdür
Bu en basit durumdur; bu durumda yaprak düğümü NULL ile değiştirin ve tahsis edilen alanı boşaltın.
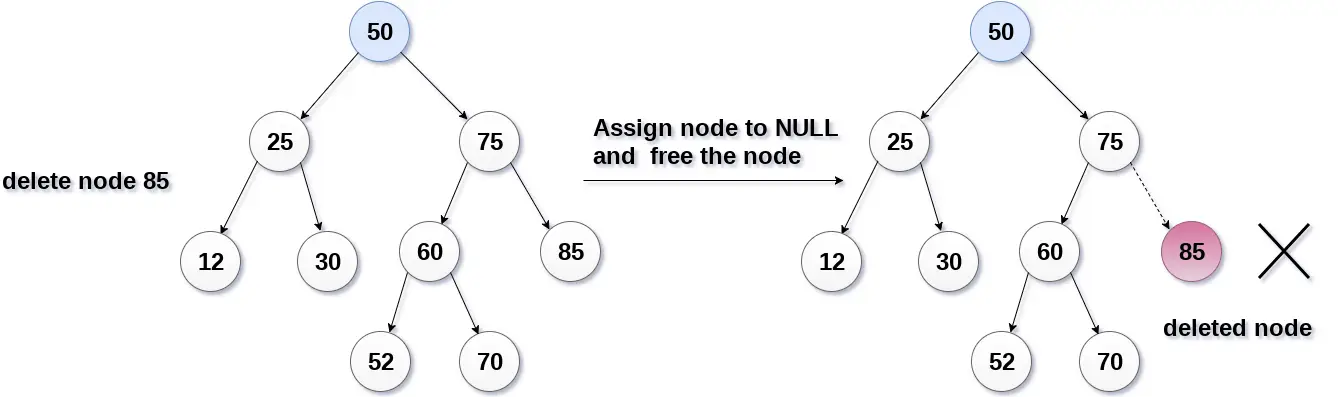
Aşağıdaki görüntüde 85 nolu düğümü siliyoruz, düğüm yaprak düğüm olduğu için düğüm NULL ile değiştirilecek ve ayrılan alan serbest bırakılacaktır.
Silinecek düğümün yalnızca bir çocuğu var.
Bu durumda, düğümü alt öğesiyle değiştirin ve artık silinecek değeri içeren alt düğümü silin. Basitçe NULL ile değiştirin ve ayrılan alanı boşaltın.
Aşağıdaki görüntüde 12 numaralı düğüm silinecek. Tek çocuğu var. Düğüm, alt düğümüyle değiştirilecek ve değiştirilen düğüm (12) (artık yaprak düğümdür) basitçe silinecektir.

Silinecek düğümün iki çocuğu var.
Diğer iki davayla karşılaştırıldığında biraz karmaşık bir dava. Ancak silinecek düğüm, (silinecek) düğüm değeri ağacın yaprağına yerleştirilene kadar yinelemeli olarak kendi sıralı halefi veya öncülüyle değiştirilir. İşlemden sonra düğümü NULL ile değiştirin ve ayrılan alanı boşaltın.
Aşağıdaki görüntüde ağacın kök düğümü olan 50 nolu düğüm silinecektir. Aşağıda verilen ağacın sıralı geçişi.
6, 25, 30, 50, 52, 60, 70, 75.
50'yi sıradaki halefi olan 52 ile değiştirin. Şimdi 50, ağacın yaprağına taşınacak ve bu da basitçe silinecek.

Algoritma
Sil (AĞAÇ, ÖĞE)
ÖĞE VERİLERİ İSE 'ağaçta öğe bulunamadı' yazın
Sil(AĞAÇ->SOL, ÖĞE)
ELSE IF ITEM > AĞAÇ -> VERİ
Sil(AĞAÇ -> SAĞ, ÖĞE)
ELSE IF TREE -> SOL VE AĞAÇ -> SAĞ
TEMP SET = findLargestNode(AĞAÇ -> SOL)
AĞAÇ AYARI -> VERİ = SICAKLIK -> VERİ
Sil(AĞAÇ -> SOL, SICAKLIK -> VERİ)
BAŞKA
SICAKLIK AYARI = AĞAÇ
IF TREE -> LEFT = NULL VE TREE -> RIGHT = NULL
AĞACI AYARLA = BOŞ
ELSE IF TREE -> LEFT != NULL
AĞAÇ AYARLA = AĞAÇ -> SOL
BAŞKA
AĞAÇ AYARLA = AĞAÇ -> SAĞ
[IF'NİN SONU]
ÜCRETSİZ SICAKLIK
[IF'NİN SONU]
İşlev:
void deletion(Node*& root, int item) { Node* parent = NULL; Node* cur = root; search(cur, item, parent); if (cur == NULL) return; if (cur->left == NULL && cur->right == NULL) { if (cur != root) { if (parent->left == cur) parent->left = NULL; else parent->right = NULL; } else root = NULL; free(cur); } else if (cur->left && cur->right) { Node* succ = findMinimum(cur- >right); int val = succ->data; deletion(root, succ->data); cur->data = val; } else { Node* child = (cur->left)? Cur- >left: cur->right; if (cur != root) { if (cur == parent->left) parent->left = child; else parent->right = child; } else root = child; free(cur); } } Node* findMinimum(Node* cur) { while(cur->left != NULL) { cur = cur->left; } return cur; } 