Bellman ford algoritması tek kaynaklı en kısa yol algoritmasıdır. Bu algoritma, ağırlıklı bir grafiğin tek bir köşesinden diğer tüm köşelerine olan en kısa mesafeyi bulmak için kullanılır. En kısa yolu bulmak için kullanılan Dijkstra algoritması vb. çeşitli algoritmalar vardır. Ağırlıklı grafik negatif ağırlık değerleri içeriyorsa Dijkstra algoritması doğru cevabı üretip üretmediğini doğrulamaz. Dijkstra algoritmasından farklı olarak Bellman ford algoritması, ağırlıklı grafik negatif ağırlık değerlerini içerse bile doğru cevabı garanti eder.
Bu algoritmanın kuralı
We will go on relaxing all the edges (n - 1) times where, n = number of vertices
Aşağıdaki grafiği göz önünde bulundurun:
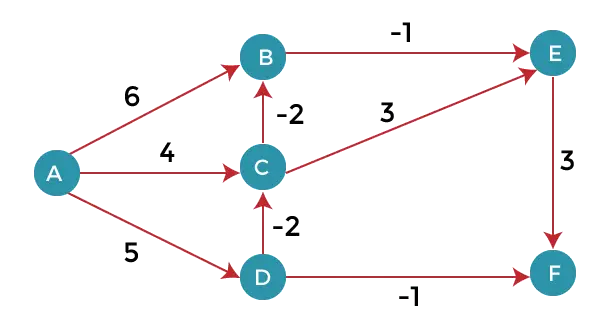
Yukarıdaki grafikte de görebileceğimiz gibi ağırlıkların bir kısmı negatiftir. Yukarıdaki grafik 6 köşe içerdiğinden 5 köşeye kadar gevşemeye devam edeceğiz. Burada tüm kenarları 5 kere gevşeteceğiz. Doğru cevaba ulaşmak için döngü 5 kez tekrarlanacaktır. Döngü 5 defadan fazla tekrarlanırsa cevap aynı olacaktır, yani köşeler arasındaki mesafede herhangi bir değişiklik olmayacaktır.
Rahatlama şu anlama gelir:
Java'da geçerli tarih
If (d(u) + c(u , v) <d(v)) d(v)="d(u)" + c(u , v) < pre> <p>To find the shortest path of the above graph, the first step is note down all the edges which are given below:</p> <p>(A, B), (A, C), (A, D), (B, E), (C, E), (D, C), (D, F), (E, F), (C, B)</p> <p>Let's consider the source vertex as 'A'; therefore, the distance value at vertex A is 0 and the distance value at all the other vertices as infinity shown as below:</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-2.webp" alt="Bellman-Ford Algorithm"> <p>Since the graph has six vertices so it will have five iterations.</p> <p> <strong>First iteration</strong> </p> <p>Consider the edge (A, B). Denote vertex 'A' as 'u' and vertex 'B' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 6</p> <p>Since (0 + 6) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 6 = 6</p> <p>Therefore, the distance of vertex B is 6.</p> <p>Consider the edge (A, C). Denote vertex 'A' as 'u' and vertex 'C' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 4</p> <p>Since (0 + 4) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 4 = 4</p> <p>Therefore, the distance of vertex C is 4.</p> <p>Consider the edge (A, D). Denote vertex 'A' as 'u' and vertex 'D' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 5</p> <p>Since (0 + 5) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 5 = 5</p> <p>Therefore, the distance of vertex D is 5.</p> <p>Consider the edge (B, E). Denote vertex 'B' as 'u' and vertex 'E' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 6</p> <p>d(v) = ∞</p> <p>c(u , v) = -1</p> <p>Since (6 - 1) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 6 - 1= 5</p> <p>Therefore, the distance of vertex E is 5.</p> <p>Consider the edge (C, E). Denote vertex 'C' as 'u' and vertex 'E' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 4</p> <p>d(v) = 5</p> <p>c(u , v) = 3</p> <p>Since (4 + 3) is greater than 5, so there will be no updation. The value at vertex E is 5.</p> <p>Consider the edge (D, C). Denote vertex 'D' as 'u' and vertex 'C' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 5</p> <p>d(v) = 4</p> <p>c(u , v) = -2</p> <p>Since (5 -2) is less than 4, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 5 - 2 = 3</p> <p>Therefore, the distance of vertex C is 3.</p> <p>Consider the edge (D, F). Denote vertex 'D' as 'u' and vertex 'F' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 5</p> <p>d(v) = ∞</p> <p>c(u , v) = -1</p> <p>Since (5 -1) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 5 - 1 = 4</p> <p>Therefore, the distance of vertex F is 4.</p> <p>Consider the edge (E, F). Denote vertex 'E' as 'u' and vertex 'F' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 5</p> <p>d(v) = ∞</p> <p>c(u , v) = 3</p> <p>Since (5 + 3) is greater than 4, so there would be no updation on the distance value of vertex F.</p> <p>Consider the edge (C, B). Denote vertex 'C' as 'u' and vertex 'B' as 'v'. Now use the relaxing formula:</p> <p>d(u) = 3</p> <p>d(v) = 6</p> <p>c(u , v) = -2</p> <p>Since (3 - 2) is less than 6, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 3 - 2 = 1</p> <p>Therefore, the distance of vertex B is 1.</p> <p>Now the first iteration is completed. We move to the second iteration.</p> <p> <strong>Second iteration:</strong> </p> <p>In the second iteration, we again check all the edges. The first edge is (A, B). Since (0 + 6) is greater than 1 so there would be no updation in the vertex B.</p> <p>The next edge is (A, C). Since (0 + 4) is greater than 3 so there would be no updation in the vertex C.</p> <p>The next edge is (A, D). Since (0 + 5) equals to 5 so there would be no updation in the vertex D.</p> <p>The next edge is (B, E). Since (1 - 1) equals to 0 which is less than 5 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(E) = d(B) +c(B , E)</p> <p>= 1 - 1 = 0</p> <p>The next edge is (C, E). Since (3 + 3) equals to 6 which is greater than 5 so there would be no updation in the vertex E.</p> <p>The next edge is (D, C). Since (5 - 2) equals to 3 so there would be no updation in the vertex C.</p> <p>The next edge is (D, F). Since (5 - 1) equals to 4 so there would be no updation in the vertex F.</p> <p>The next edge is (E, F). Since (5 + 3) equals to 8 which is greater than 4 so there would be no updation in the vertex F.</p> <p>The next edge is (C, B). Since (3 - 2) equals to 1` so there would be no updation in the vertex B.</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-3.webp" alt="Bellman-Ford Algorithm"> <p> <strong>Third iteration</strong> </p> <p>We will perform the same steps as we did in the previous iterations. We will observe that there will be no updation in the distance of vertices.</p> <pre> The following are the distances of vertices: A: 0 B: 1 C: 3 D: 5 E: 0 F: 3 </pre> <p> <strong>Time Complexity</strong> </p> <p>The time complexity of Bellman ford algorithm would be O(E|V| - 1).</p> <pre> function bellmanFord(G, S) for each vertex V in G distance[V] <- 0 infinite previous[v] <- null distance[s] for each vertex v in g edge (u,v) tempdistance distance[u] + edge_weight(u, v) if < distance[v] u distance[v} error: negative cycle exists return distance[], previous[] pre> <p> <strong>Drawbacks of Bellman ford algorithm</strong> </p> <ul> <li>The bellman ford algorithm does not produce a correct answer if the sum of the edges of a cycle is negative. Let's understand this property through an example. Consider the below graph. <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-4.webp" alt="Bellman-Ford Algorithm"></li> <li>In the above graph, we consider vertex 1 as the source vertex and provides 0 value to it. We provide infinity value to other vertices shown as below: <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-5.webp" alt="Bellman-Ford Algorithm"> <br>Edges can be written as: <br> (1, 3), (1, 2), (2, 4), (3, 2), (4, 3) </li> </ul> <p> <strong>First iteration</strong> </p> <p> <strong>Consider the edge (1, 3). Denote vertex '1' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 5</p> <p>Since (0 + 5) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 5 = 5</p> <p>Therefore, the distance of vertex 3 is 5.</p> <p> <strong>Consider the edge (1, 2). Denote vertex '1' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 4</p> <p>Since (0 + 4) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 4 = 4</p> <p>Therefore, the distance of vertex 2 is 4.</p> <p> <strong>Consider the edge (3, 2). Denote vertex '3' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 5</p> <p>d(v) = 4</p> <p>c(u , v) = 7</p> <p>Since (5 + 7) is greater than 4, so there would be no updation in the vertex 2.</p> <p> <strong>Consider the edge (2, 4). Denote vertex '2' as 'u' and vertex '4' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 4</p> <p>d(v) = ∞</p> <p>c(u , v) = 7</p> <p>Since (4 + 7) equals to 11 which is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 4 + 7 = 11</p> <p>Therefore, the distance of vertex 4 is 11.</p> <p> <strong>Consider the edge (4, 3). Denote vertex '4' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 11</p> <p>d(v) = 5</p> <p>c(u , v) = -15</p> <p>Since (11 - 15) equals to -4 which is less than 5, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 11 - 15 = -4</p> <p>Therefore, the distance of vertex 3 is -4.</p> <p>Now we move to the second iteration.</p> <p> <strong>Second iteration</strong> </p> <p>Now, again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -4 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-4 + 7) equals to 3 which is less than 4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -4 + 7 = 3</p> <p>Therefore, the value at vertex 2 is 3.</p> <p>The next edge is (2, 4). Since ( 3+7) equals to 10 which is less than 11 so update</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 3 + 7 = 10</p> <p>Therefore, the value at vertex 4 is 10.</p> <p>The next edge is (4, 3). Since (10 - 15) equals to -5 which is less than -4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 10 - 15 = -5</p> <p>Therefore, the value at vertex 3 is -5.</p> <p>Now we move to the third iteration.</p> <p> <strong>Third iteration</strong> </p> <p>Now again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -5 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 which is greater than 3 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-5 + 7) equals to 2 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -5 + 7 = 2</p> <p>Therefore, the value at vertex 2 is 2.</p> <p>The next edge is (2, 4). Since (2 + 7) equals to 9 which is less than 10 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 2 + 7 = 9</p> <p>Therefore, the value at vertex 4 is 9.</p> <p>The next edge is (4, 3). Since (9 - 15) equals to -6 which is less than -5 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 9 - 15 = -6</p> <p>Therefore, the value at vertex 3 is -6.</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-6.webp" alt="Bellman-Ford Algorithm"> <p>Since the graph contains 4 vertices, so according to the bellman ford algorithm, there would be only 3 iterations. If we try to perform 4<sup>th</sup> iteration on the graph, the distance of the vertices from the given vertex should not change. If the distance varies, it means that the bellman ford algorithm is not providing the correct answer.</p> <p> <strong>4<sup>th</sup> iteration</strong> </p> <p>The first edge is (1, 3). Since (0 +5) equals to 5 which is greater than -6 so there would be no change in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) is greater than 2 so there would be no updation.</p> <p>The next edge is (3, 2). Since (-6 + 7) equals to 1 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -6 + 7 = 1</p> <p>In this case, the value of the vertex is updated. So, we conclude that the bellman ford algorithm does not work when the graph contains the negative weight cycle.</p> <p>Therefore, the value at vertex 2 is 1.</p> <hr></-></pre></d(v))>
d(v) = 0 + 6 = 6
Bu nedenle B köşesinin mesafesi 6'dır.
(A, C) kenarını düşünün. 'A' köşesini 'u' ve 'C' köşesini 'v' olarak belirtin. Şimdi rahatlatıcı formülü kullanın:
d(u) = 0
d(v) = ∞
c(u , v) = 4
(0 + 4) ∞'dan küçük olduğundan güncelleme
d(v) = d(u) + c(u , v)
d(v) = 0 + 4 = 4
Bu nedenle C köşesinin mesafesi 4'tür.
(A, D) kenarını düşünün. 'A' köşesini 'u' ve 'D' köşesini 'v' olarak belirtin. Şimdi rahatlatıcı formülü kullanın:
d(u) = 0
d(v) = ∞
c(u , v) = 5
(0 + 5) ∞'dan küçük olduğundan güncelleme
d(v) = d(u) + c(u , v)
d(v) = 0 + 5 = 5
Bu nedenle D köşesinin mesafesi 5'tir.
(B, E) kenarını düşünün. 'B' köşesini 'u' ve 'E' köşesini 'v' olarak belirtin. Şimdi rahatlatıcı formülü kullanın:
d(u) = 6
d(v) = ∞
c(u , v) = -1
(6 - 1) ∞'dan küçük olduğundan güncelleyin
d(v) = d(u) + c(u , v)
d(v) = 6 - 1= 5
Bu nedenle E köşesinin mesafesi 5'tir.
(C, E) kenarını düşünün. 'C' köşesini 'u' ve 'E' köşesini 'v' olarak belirtin. Şimdi rahatlatıcı formülü kullanın:
d(u) = 4
d(v) = 5
c(u , v) = 3
(4 + 3) 5'ten büyük olduğundan güncelleme yapılmayacaktır. E köşesindeki değer 5'tir.
(D, C) kenarını düşünün. 'D' köşesini 'u' ve 'C' köşesini 'v' olarak belirtin. Şimdi rahatlatıcı formülü kullanın:
d(u) = 5
d(v) = 4
c(u , v) = -2
(5 -2) 4'ten küçük olduğundan güncelleyin
d(v) = d(u) + c(u , v)
d(v) = 5 - 2 = 3
Bu nedenle C köşesinin mesafesi 3'tür.
(D, F) kenarını düşünün. 'D' köşesini 'u' ve 'F' köşesini 'v' olarak belirtin. Şimdi rahatlatıcı formülü kullanın:
d(u) = 5
d(v) = ∞
c(u , v) = -1
(5 -1) ∞'dan küçük olduğundan güncelleyin
d(v) = d(u) + c(u , v)
d(v) = 5 - 1 = 4
Bu nedenle F köşesinin mesafesi 4'tür.
(E, F) kenarını düşünün. 'E' köşesini 'u' ve 'F' köşesini 'v' olarak belirtin. Şimdi rahatlatıcı formülü kullanın:
d(u) = 5
d(v) = ∞
c(u , v) = 3
(5 + 3) 4'ten büyük olduğundan F köşesinin uzaklık değerinde bir güncelleme olmayacaktır.
(C, B) kenarını düşünün. 'C' köşesini 'u' ve 'B' köşesini 'v' olarak belirtin. Şimdi rahatlatıcı formülü kullanın:
d(u) = 3
d(v) = 6
c(u , v) = -2
(3 - 2) 6'dan küçük olduğundan güncelleyin
d(v) = d(u) + c(u , v)
d(v) = 3 - 2 = 1
Bu nedenle B köşesinin mesafesi 1'dir.
Artık ilk yineleme tamamlandı. İkinci yinelemeye geçiyoruz.
İkinci yineleme:
bilgisayarı hızlı yapan şey nedir
İkinci yinelemede tüm kenarları tekrar kontrol ediyoruz. İlk kenar (A, B)'dir. (0 + 6) 1'den büyük olduğundan B köşesinde güncelleme olmayacaktır.
Bir sonraki kenar (A, C)'dir. (0 + 4) 3'ten büyük olduğundan C köşesinde herhangi bir güncelleme olmayacaktır.
Bir sonraki kenar (A, D)'dir. (0 + 5) 5'e eşit olduğundan, D köşesinde herhangi bir güncelleme olmayacaktır.
Bir sonraki kenar (B, E)'dir. (1 - 1) 0'a eşit olduğundan, yani 5'ten küçük olduğundan güncelleyin:
d(v) = d(u) + c(u, v)
d(E) = d(B) +c(B , E)
= 1 - 1 = 0
Bir sonraki kenar (C, E)'dir. (3 + 3), 5'ten büyük olan 6'ya eşit olduğundan, E tepe noktasında herhangi bir güncelleme olmayacaktır.
Bir sonraki kenar (D, C)'dir. (5 - 2) 3'e eşit olduğundan, C köşesinde herhangi bir güncelleme olmayacaktır.
Bir sonraki kenar (D, F)'dir. (5 - 1) 4'e eşit olduğundan, F tepe noktasında herhangi bir güncelleme olmayacaktır.
Bir sonraki kenar (E, F)'dir. (5 + 3), 4'ten büyük olan 8'e eşit olduğundan, F tepe noktasında herhangi bir güncelleme olmayacaktır.
Bir sonraki kenar (C, B)'dir. (3 - 2) 1`'e eşit olduğundan B köşe noktasında herhangi bir güncelleme olmayacaktır.

Üçüncü yineleme
Önceki yinelemelerde yaptığımız adımların aynısını gerçekleştireceğiz. Köşelerin uzaklığında herhangi bir güncelleme olmayacağını gözlemleyeceğiz.
The following are the distances of vertices: A: 0 B: 1 C: 3 D: 5 E: 0 F: 3
Zaman Karmaşıklığı
Bellman ford algoritmasının zaman karmaşıklığı O(E|V| - 1) olacaktır.
function bellmanFord(G, S) for each vertex V in G distance[V] <- 0 infinite previous[v] <- null distance[s] for each vertex v in g edge (u,v) tempdistance distance[u] + edge_weight(u, v) if < distance[v] u distance[v} error: negative cycle exists return distance[], previous[] pre> <p> <strong>Drawbacks of Bellman ford algorithm</strong> </p> <ul> <li>The bellman ford algorithm does not produce a correct answer if the sum of the edges of a cycle is negative. Let's understand this property through an example. Consider the below graph. <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-4.webp" alt="Bellman-Ford Algorithm"></li> <li>In the above graph, we consider vertex 1 as the source vertex and provides 0 value to it. We provide infinity value to other vertices shown as below: <br> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-5.webp" alt="Bellman-Ford Algorithm"> <br>Edges can be written as: <br> (1, 3), (1, 2), (2, 4), (3, 2), (4, 3) </li> </ul> <p> <strong>First iteration</strong> </p> <p> <strong>Consider the edge (1, 3). Denote vertex '1' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 5</p> <p>Since (0 + 5) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 5 = 5</p> <p>Therefore, the distance of vertex 3 is 5.</p> <p> <strong>Consider the edge (1, 2). Denote vertex '1' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 0</p> <p>d(v) = ∞</p> <p>c(u , v) = 4</p> <p>Since (0 + 4) is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 0 + 4 = 4</p> <p>Therefore, the distance of vertex 2 is 4.</p> <p> <strong>Consider the edge (3, 2). Denote vertex '3' as 'u' and vertex '2' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 5</p> <p>d(v) = 4</p> <p>c(u , v) = 7</p> <p>Since (5 + 7) is greater than 4, so there would be no updation in the vertex 2.</p> <p> <strong>Consider the edge (2, 4). Denote vertex '2' as 'u' and vertex '4' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 4</p> <p>d(v) = ∞</p> <p>c(u , v) = 7</p> <p>Since (4 + 7) equals to 11 which is less than ∞, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 4 + 7 = 11</p> <p>Therefore, the distance of vertex 4 is 11.</p> <p> <strong>Consider the edge (4, 3). Denote vertex '4' as 'u' and vertex '3' as 'v'. Now use the relaxing formula:</strong> </p> <p>d(u) = 11</p> <p>d(v) = 5</p> <p>c(u , v) = -15</p> <p>Since (11 - 15) equals to -4 which is less than 5, so update</p> <pre> d(v) = d(u) + c(u , v) </pre> <p>d(v) = 11 - 15 = -4</p> <p>Therefore, the distance of vertex 3 is -4.</p> <p>Now we move to the second iteration.</p> <p> <strong>Second iteration</strong> </p> <p>Now, again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -4 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-4 + 7) equals to 3 which is less than 4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -4 + 7 = 3</p> <p>Therefore, the value at vertex 2 is 3.</p> <p>The next edge is (2, 4). Since ( 3+7) equals to 10 which is less than 11 so update</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 3 + 7 = 10</p> <p>Therefore, the value at vertex 4 is 10.</p> <p>The next edge is (4, 3). Since (10 - 15) equals to -5 which is less than -4 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 10 - 15 = -5</p> <p>Therefore, the value at vertex 3 is -5.</p> <p>Now we move to the third iteration.</p> <p> <strong>Third iteration</strong> </p> <p>Now again we will check all the edges. The first edge is (1, 3). Since (0 + 5) equals to 5 which is greater than -5 so there would be no updation in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) equals to 4 which is greater than 3 so there would be no updation in the vertex 2.</p> <p>The next edge is (3, 2). Since (-5 + 7) equals to 2 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -5 + 7 = 2</p> <p>Therefore, the value at vertex 2 is 2.</p> <p>The next edge is (2, 4). Since (2 + 7) equals to 9 which is less than 10 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(4) = d(2) +c(2, 4)</p> <p>= 2 + 7 = 9</p> <p>Therefore, the value at vertex 4 is 9.</p> <p>The next edge is (4, 3). Since (9 - 15) equals to -6 which is less than -5 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(3) = d(4) +c(4, 3)</p> <p>= 9 - 15 = -6</p> <p>Therefore, the value at vertex 3 is -6.</p> <img src="//techcodeview.com/img/daa-tutorial/85/bellman-ford-algorithm-6.webp" alt="Bellman-Ford Algorithm"> <p>Since the graph contains 4 vertices, so according to the bellman ford algorithm, there would be only 3 iterations. If we try to perform 4<sup>th</sup> iteration on the graph, the distance of the vertices from the given vertex should not change. If the distance varies, it means that the bellman ford algorithm is not providing the correct answer.</p> <p> <strong>4<sup>th</sup> iteration</strong> </p> <p>The first edge is (1, 3). Since (0 +5) equals to 5 which is greater than -6 so there would be no change in the vertex 3.</p> <p>The next edge is (1, 2). Since (0 + 4) is greater than 2 so there would be no updation.</p> <p>The next edge is (3, 2). Since (-6 + 7) equals to 1 which is less than 3 so update:</p> <p>d(v) = d(u) + c(u, v)</p> <p>d(2) = d(3) +c(3, 2)</p> <p>= -6 + 7 = 1</p> <p>In this case, the value of the vertex is updated. So, we conclude that the bellman ford algorithm does not work when the graph contains the negative weight cycle.</p> <p>Therefore, the value at vertex 2 is 1.</p> <hr></->
d(v) = 0 + 5 = 5
Bu nedenle köşe 3'ün mesafesi 5'tir.
(1, 2) kenarını düşünün. '1' köşesini 'u' ve '2' köşesini 'v' olarak belirtin. Şimdi rahatlatıcı formülü kullanın:
d(u) = 0
d(v) = ∞
c(u , v) = 4
(0 + 4) ∞'dan küçük olduğundan güncelleme
d(v) = d(u) + c(u , v)
d(v) = 0 + 4 = 4
Bu nedenle köşe 2'nin mesafesi 4'tür.
(3, 2) kenarını düşünün. '3' köşesini 'u' ve '2' köşesini 'v' olarak belirtin. Şimdi rahatlatıcı formülü kullanın:
d(u) = 5
d(v) = 4
c(u , v) = 7
(5 + 7) 4'ten büyük olduğundan 2. köşede güncelleme olmayacaktır.
(2, 4) kenarını düşünün. '2' köşesini 'u' ve '4' köşesini 'v' olarak belirtin. Şimdi rahatlatıcı formülü kullanın:
d(u) = 4
d(v) = ∞
c(u , v) = 7
(4 + 7) ∞'dan küçük olan 11'e eşit olduğundan güncelleyin
d(v) = d(u) + c(u , v)
d(v) = 4 + 7 = 11
Bu nedenle 4. köşenin mesafesi 11'dir.
(4, 3) kenarını düşünün. '4' köşesini 'u' ve '3' köşesini 'v' olarak belirtin. Şimdi rahatlatıcı formülü kullanın:
d(u) = 11
d(v) = 5
c(u , v) = -15
(11 - 15), 5'ten küçük olan -4'e eşit olduğundan güncelleyin
d(v) = d(u) + c(u , v)
d(v) = 11 - 15 = -4
Bu nedenle köşe 3'ün mesafesi -4'tür.
Şimdi ikinci yinelemeye geçiyoruz.
İkinci yineleme
Şimdi yine tüm kenarları kontrol edeceğiz. İlk kenar (1, 3)'tür. (0 + 5) -4'ten büyük olan 5'e eşit olduğundan, 3. köşede güncelleme olmayacaktır.
Bir sonraki kenar (1, 2)'dir. (0 + 4) 4'e eşit olduğundan 2. köşede güncelleme olmayacaktır.
Bir sonraki kenar (3, 2)'dir. (-4 + 7), 4'ten küçük olan 3'e eşit olduğundan güncelleyin:
d(v) = d(u) + c(u, v)
dizeyi karaktere dönüştür
d(2) = d(3) +c(3, 2)
= -4 + 7 = 3
Bu nedenle 2. köşedeki değer 3'tür.
Bir sonraki kenar (2, 4)'tür. ( 3+7) 10'a eşit olduğundan ve bu da 11'den küçük olduğundan güncelleyin
d(v) = d(u) + c(u, v)
d(4) = d(2) +c(2, 4)
= 3 + 7 = 10
Bu nedenle 4. köşedeki değer 10'dur.
Java dizesi içerir
Bir sonraki kenar (4, 3)'tür. (10 - 15) -5'e eşit olduğundan -4'ten küçüktür, bu nedenle güncelleyin:
d(v) = d(u) + c(u, v)
d(3) = d(4) +c(4, 3)
= 10 - 15 = -5
Bu nedenle 3. köşedeki değer -5'tir.
Şimdi üçüncü yinelemeye geçiyoruz.
Üçüncü yineleme
Şimdi tekrar tüm kenarları kontrol edeceğiz. İlk kenar (1, 3)'tür. (0 + 5) -5'ten büyük olan 5'e eşit olduğundan, 3. köşede güncelleme olmayacaktır.
Bir sonraki kenar (1, 2)'dir. (0 + 4) 3'ten büyük olan 4'e eşit olduğundan, 2. köşede güncelleme olmayacaktır.
Bir sonraki kenar (3, 2)'dir. (-5 + 7), 3'ten küçük olan 2'ye eşit olduğundan güncelleyin:
d(v) = d(u) + c(u, v)
d(2) = d(3) +c(3, 2)
= -5 + 7 = 2
Bu nedenle 2. köşedeki değer 2'dir.
Bir sonraki kenar (2, 4)'tür. (2 + 7) 10'dan küçük olan 9'a eşit olduğundan güncelleyin:
d(v) = d(u) + c(u, v)
d(4) = d(2) +c(2, 4)
= 2 + 7 = 9
Bu nedenle 4. köşedeki değer 9'dur.
Bir sonraki kenar (4, 3)'tür. (9 - 15) -6'ya eşit olduğundan ve bu da -5'ten küçük olduğundan güncelleyin:
d(v) = d(u) + c(u, v)
d(3) = d(4) +c(4, 3)
= 9 - 15 = -6
Bu nedenle 3. köşedeki değer -6'dır.

Grafik 4 köşe içerdiğinden bellman ford algoritmasına göre yalnızca 3 yineleme olacaktır. 4'ü gerçekleştirmeye çalışırsakoGrafik yinelendiğinde, köşelerin verilen tepe noktasından uzaklığı değişmemelidir. Mesafe değişiyorsa bu, bellman ford algoritmasının doğru cevabı vermediği anlamına gelir.
4oyineleme
İlk kenar (1, 3)'tür. (0 +5) -6'dan büyük olan 5'e eşit olduğundan 3. köşede herhangi bir değişiklik olmayacaktır.
Bir sonraki kenar (1, 2)'dir. (0 + 4) 2'den büyük olduğundan güncelleme yapılmayacaktır.
Bir sonraki kenar (3, 2)'dir. (-6 + 7), 3'ten küçük olan 1'e eşit olduğundan güncelleyin:
d(v) = d(u) + c(u, v)
d(2) = d(3) +c(3, 2)
= -6 + 7 = 1
Bu durumda köşenin değeri güncellenir. Dolayısıyla grafik negatif ağırlık döngüsünü içerdiğinde bellman ford algoritmasının çalışmadığı sonucuna varıyoruz.
Bu nedenle 2. köşedeki değer 1'dir.
