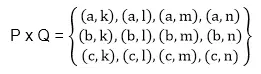Birleşim, kesişim ve tümleyen işlemleri altındaki kümeler, Tablo 1'de listelenen çeşitli yasaları (özdeşlikleri) karşılar.
Tablo: Kümelerin Cebir Yasası
| Bağımsız Kanunlar | (a) Bir ∪ Bir = Bir | (b) Bir ∩ Bir = Bir |
| Birleşme Kanunları | (a) (A ∪ B) ∪ C = Bir ∪ (B ∪ C) | (b) (Bir ∩ B) ∩ C = Bir ∩ (B ∩ C) |
| Değişmeli Kanunlar | (a) Bir ∪ B = B ∪ Bir | (b) Bir ∩ B = B ∩ Bir |
| Dağıtım Kanunları | (a) Bir ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) | (b) Bir ∩ (B ∪ C) =(A ∩ B) ∪ (A ∩ C) |
| De Morgan Kanunları | (a) (A ∪B)C=AC∩BC | (b) (A ∩B)C=AC∪BC |
| Kimlik Kanunları | (a) Bir ∪ ∅ = Bir (b) Bir ∪ U = U | (c) Bir ∩ U =A (d) Bir ∩ ∅ = ∅ |
| Tamamlayıcı Kanunlar | (a) Bir ∪ BirC= sen (b) Bir ∩ BirC= ∅ | (c) ÜC= ∅ (d) ∅C= sen |
| İnvolüsyon Yasası | (bir) (birC)C= bir |
Tablo 1 kümelerin cebir yasasını göstermektedir.
Örnek 1: İdempotent Yasaları Kanıtlayın:
(a) A ∪ A = A
Çözüm:
Since, B ⊂ A ∪ B, therefore A ⊂ A ∪ A Let x ∈ A ∪ A ⇒ x ∈ A or x ∈ A ⇒ x ∈ A ∴ A ∪ A ⊂ A As A ∪ A ⊂ A and A ⊂ A ∪ A ⇒ A =A ∪ A. Hence Proved.
(b) A ∩ A = A
Çözüm:
Since, A ∩ B ⊂ B, therefore A ∩ A ⊂ A Let x ∈ A ⇒ x ∈ A and x ∈ A ⇒ x ∈ A ∩ A ∴ A ⊂ A ∩ A As A ∩ A ⊂ A and A ⊂ A ∩ A ⇒ A = A ∩ A. Hence Proved.
Örnek 2: İlişkisel Yasaları Kanıtlayın:
(a) (A ∪ B) ∪ C = A ∪ (B ∪ C)
Çözüm:
Let some x ∈ (A'∪ B) ∪ C ⇒ (x ∈ A or x ∈ B) or x ∈ C ⇒ x ∈ A or x ∈ B or x ∈ C ⇒ x ∈ A or (x ∈ B or x ∈ C) ⇒ x ∈ A or x ∈ B ∪ C ⇒ x ∈ A ∪ (B ∪ C). Similarly, if some x ∈ A ∪ (B ∪ C), then x ∈ (A ∪ B) ∪ C. Thus, any x ∈ A ∪ (B ∪ C) ⇔ x ∈ (A ∪ B) ∪ C. Hence Proved.
(b) (A ∩ B) ∩ C = A ∩ (B ∩ C)
Çözüm:
Let some x ∈ A ∩ (B ∩ C) ⇒ x ∈ A and x ∈ B ∩ C ⇒ x ∈ A and (x ∈ B and x ∈ C) ⇒ x ∈ A and x ∈ B and x ∈ C ⇒ (x ∈ A and x ∈ B) and x ∈ C) ⇒ x ∈ A ∩ B and x ∈ C ⇒ x ∈ (A ∩ B) ∩ C. Similarly, if some x ∈ A ∩ (B ∩ C), then x ∈ (A ∩ B) ∩ C Thus, any x ∈ (A ∩ B) ∩ C ⇔ x ∈ A ∩ (B ∩ C). Hence Proved.
Örnek3: Değişmeli Yasaları Kanıtlayın
(a) A ∪ B = B ∪ A
Çözüm:
To Prove A ∪ B = B ∪ A A ∪ B = {x: x ∈ A or x ∈ B} = {x: x ∈ B or x ∈ A} (∵ Order is not preserved in case of sets) A ∪ B = B ∪ A. Hence Proved. (b) A ∩ B = B ∩ A
Çözüm:
To Prove A ∩ B = B ∩ A A ∩ B = {x: x ∈ A and x ∈ B} = {x: x ∈ B and x ∈ A} (∵ Order is not preserved in case of sets) A ∩ B = B ∩ A. Hence Proved. Örnek 4: Dağıtım Yasalarını Kanıtlayın
(a) A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
Çözüm:
To Prove Let x ∈ A ∪ (B ∩ C) ⇒ x ∈ A or x ∈ B ∩ C ⇒ (x ∈ A or x ∈ A) or (x ∈ B and x ∈ C) ⇒ (x ∈ A or x ∈ B) and (x ∈ A or x ∈ C) ⇒ x ∈ A ∪ B and x ∈ A ∪ C ⇒ x ∈ (A ∪ B) ∩ (A ∪ C) Therefore, A ∪ (B ∩ C) ⊂ (A ∪ B) ∩ (A ∪ C)............(i) Again, Let y ∈ (A ∪ B) ∩ (A ∪ C) ⇒ y ∈ A ∪ B and y ∈ A ∪ C ⇒ (y ∈ A or y ∈ B) and (y ∈ A or y ∈ C) ⇒ (y ∈ A and y ∈ A) or (y ∈ B and y ∈ C) ⇒ y ∈ A or y ∈ B ∩ C ⇒ y ∈ A ∪ (B ∩ C) Therefore, (A ∪ B) ∩ (A ∪ C) ⊂ A ∪ (B ∩ C)............(ii) Combining (i) and (ii), we get A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C). Hence Proved
(b) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
Çözüm:
To Prove Let x ∈ A ∩ (B ∪ C) ⇒ x ∈ A and x ∈ B ∪ C ⇒ (x ∈ A and x ∈ A) and (x ∈ B or x ∈ C) ⇒ (x ∈ A and x ∈ B) or (x ∈ A and x ∈ C) ⇒ x ∈ A ∩ B or x ∈ A ∩ C ⇒ x ∈ (A ∩ B) ∪ (A ∪ C) Therefore, A ∩ (B ∪ C) ⊂ (A ∩ B) ∪ (A ∪ C)............ (i) Again, Let y ∈ (A ∩ B) ∪ (A ∪ C) ⇒ y ∈ A ∩ B or y ∈ A ∩ C ⇒ (y ∈ A and y ∈ B) or (y ∈ A and y ∈ C) ⇒ (y ∈ A or y ∈ A) and (y ∈ B or y ∈ C) ⇒ y ∈ A and y ∈ B ∪ C ⇒ y ∈ A ∩ (B ∪ C) Therefore, (A ∩ B) ∪ (A ∪ C) ⊂ A ∩ (B ∪ C)............ (ii) Combining (i) and (ii), we get A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∪ C). Hence Proved
Örnek 5: De Morgan Yasalarını Kanıtlayın
(a) (A ∪B)<sup>c</sup>=A<sup>c</sup>∩ B<sup>c</sup>
Çözüm:
To Prove (A ∪B)<sup>c</sup>=A<sup>c</sup>∩ B<sup>c</sup> Let x ∈ (A ∪B)<sup>c</sup> ⇒ x ∉ A ∪ B (∵ a ∈ A ⇔ a ∉ A<sup>c</sup>) ⇒ x ∉ A and x ∉ B ⇒ x ∉ A<sup>c</sup> and x ∉ B<sup>c</sup> ⇒ x ∉ A<sup>c</sup>∩ B<sup>c</sup> Therefore, (A ∪B)<sup>c</sup> ⊂ A<sup>c</sup>∩ B<sup>c</sup>............. (i) Again, let x ∈ A<sup>c</sup>∩ B<sup>c</sup> ⇒ x ∈ A<sup>c</sup> and x ∈ B<sup>c</sup> ⇒ x ∉ A and x ∉ B ⇒ x ∉ A ∪ B ⇒ x ∈ (A ∪B)<sup>c</sup> Therefore, A<sup>c</sup>∩ B<sup>c</sup> ⊂ (A ∪B)<sup>c</sup>............. (ii) Combining (i) and (ii), we get A<sup>c</sup>∩ B<sup>c</sup> =(A ∪B)<sup>c</sup>. Hence Proved.
(b) (A ∩B)<sup>c</sup> = A<sup>c</sup>∪ B<sup>c</sup>
Çözüm:
Let x ∈ (A ∩B)<sup>c</sup> ⇒ x ∉ A ∩ B (∵ a ∈ A ⇔ a ∉ A<sup>c</sup>) ⇒ x ∉ A or x ∉ B ⇒ x ∈ A<sup>c</sup> and x ∈ B<sup>c</sup> ⇒ x ∈ A<sup>c</sup>∪ B<sup>c</sup> ∴ (A ∩B)<sup>c</sup>⊂ (A ∪B)<sup>c</sup>.................. (i) Again, Let x ∈ A<sup>c</sup>∪ B<sup>c</sup> ⇒ x ∈ A<sup>c</sup> or x ∈ B<sup>c</sup> ⇒ x ∉ A or x ∉ B ⇒ x ∉ A ∩ B ⇒ x ∈ (A ∩B)<sup>c</sup> ∴ A<sup>c</sup>∪ B<sup>c</sup>⊂ (A ∩B)<sup>c</sup>.................... (ii) Combining (i) and (ii), we get(A ∩B)<sup>c</sup>=A<sup>c</sup>∪ B<sup>c</sup>. Hence Proved.
Örnek 6: Kimlik Yasalarını Kanıtlayın.
(a) A ∪ ∅ = A
Çözüm:
To Prove A ∪ ∅ = A Let x ∈ A ∪ ∅ ⇒ x ∈ A or x ∈ ∅ ⇒ x ∈ A (∵x ∈ ∅, as ∅ is the null set ) Therefore, x ∈ A ∪ ∅ ⇒ x ∈ A Hence, A ∪ ∅ ⊂ A. We know that A ⊂ A ∪ B for any set B. But for B = ∅, we have A ⊂ A ∪ ∅ From above, A ⊂ A ∪ ∅ , A ∪ ∅ ⊂ A ⇒ A = A ∪ ∅. Hence Proved.
(b) A ∩ ∅ = ∅
Çözüm:
To Prove A ∩ ∅ = ∅ If x ∈ A, then x ∉ ∅ (∵∅ is a null set) Therefore, x ∈ A, x ∉ ∅ ⇒ A ∩ ∅ = ∅. Hence Proved.
(c) A ∪ U = U
Çözüm:
To Prove A ∪ U = U Every set is a subset of a universal set. ∴ A ∪ U ⊆ U Also, U ⊆ A ∪ U Therefore, A ∪ U = U. Hence Proved.
(d) A ∩ U = A
Çözüm:
To Prove A ∩ U = A We know A ∩ U ⊂ A................. (i) So we have to show that A ⊂ A ∩ U Let x ∈ A ⇒ x ∈ A and x ∈ U (∵ A ⊂ U so x ∈ A ⇒ x ∈ U ) ∴ x ∈ A ⇒ x ∈ A ∩ U ∴ A ⊂ A ∩ U................. (ii) From (i) and (ii), we get A ∩ U = A. Hence Proved.
Örnek7: Tamamlayıcı Yasaları Kanıtlayın
(a) A ∪ A<sup>c</sup>= U
Çözüm:
To Prove A ∪ A<sup>c</sup>= U Every set is a subset of U ∴ A ∪ A<sup>c</sup> ⊂ U.................. (i) We have to show that U ⊆ A ∪ A<sup>c</sup> Let x ∈ U ⇒ x ∈ A or x ∉ A ⇒ x ∈ A or x ∈ A<sup>c</sup> ⇒ x ∈ A ∪ A<sup>c</sup> ∴ U ⊆ A ∪ A<sup>c</sup>................... (ii) From (i) and (ii), we get A ∪ A<sup>c</sup>= U. Hence Proved.
(b) A ∩ A<sup>c</sup>=∅
Çözüm:
As ∅ is the subset of every set ∴ ∅ ⊆ A ∩ A<sup>c</sup>..................... (i) We have to show that A ∩ A<sup>c</sup> ⊆ ∅ Let x ∈ A ∩ A<sup>c</sup> ⇒ x ∈ A and x ∈ A<sup>c</sup> ⇒ x ∈ A and x ∉ A ⇒ x ∈ ∅ ∴ A ∩ A<sup>c</sup> ⊂∅..................... (ii) From (i) and (ii), we get A∩ A<sup>c</sup>=∅. Hence Proved.
(c) U<sup>c</sup>= ∅
Çözüm:
Let x ∈ U<sup>c</sup> ⇔ x ∉ U ⇔ x ∈ ∅ ∴ U<sup>c</sup>= ∅. Hence Proved. (As U is the Universal Set).
(d) ∅<sup>c</sup> = U
Çözüm:
Let x ∈ ∅<sup>c</sup> ⇔ x ∉ ∅ ⇔ x ∈ U (As ∅ is an empty set) ∴ ∅<sup>c</sup> = U. Hence Proved.
Örnek8: Evrim Yasasını Kanıtlayın
(a) (A<sup>c</sup> )<sup>c</sup> A.
Çözüm:
Let x ∈ (A<sup>c</sup> )<sup>c</sup> ⇔ x ∉ A<sup>c</sup>⇔ x ∈ a ∴ (A<sup>c</sup> )<sup>c</sup> =A. Hence Proved.
İkilik:
E'nin ikili E∗'si, E'deki her ∪, ∩, U ve ∅ oluşumunu sırasıyla ∩, ∪, ∅ ve U ile değiştirerek elde edilen denklemdir. Örneğin, ikili
(U ∩ A) ∪ (B ∩ A) = A is (∅ ∪ A) ∩ (B ∪ A) = A
İkilik ilkesi olarak, eğer herhangi bir E denklemi bir özdeşlik ise, o zaman onun ikili E∗'sinin de bir özdeşlik olduğu belirtilmektedir.
Uzatma Prensibi:
Genişleme ilkesine göre iki küme A ve B ancak ve ancak aynı elemanlara sahip olmaları durumunda aynıdır. Eşit kümeleri A=B ile gösteriyoruz.
If A= {1, 3, 5} and B= {3, 1, 5}, then A=B i.e., A and B are equal sets. If A= {1, 4, 7} and B= {5, 4, 8}, then A≠ B i.e.., A and B are unequal sets. İki kümenin kartezyen çarpımı:
Bu sırayla iki P ve Q kümesinin Kartezyen Çarpımı, ilk üyesi P kümesine ve ikinci üyesi Q kümesine ait olan ve P x Q ile gösterilen tüm sıralı çiftlerin kümesidir, yani,
harita java yineleyici
P x Q = {(x, y): x ∈ P, y ∈ Q}. Örnek: P = {a, b, c} ve Q = {k, l, m, n} olsun. P ve Q'nun Kartezyen çarpımını belirleyin.
Çözüm: P ve Q'nun Kartezyen çarpımı